Progression of Early Number and Counting
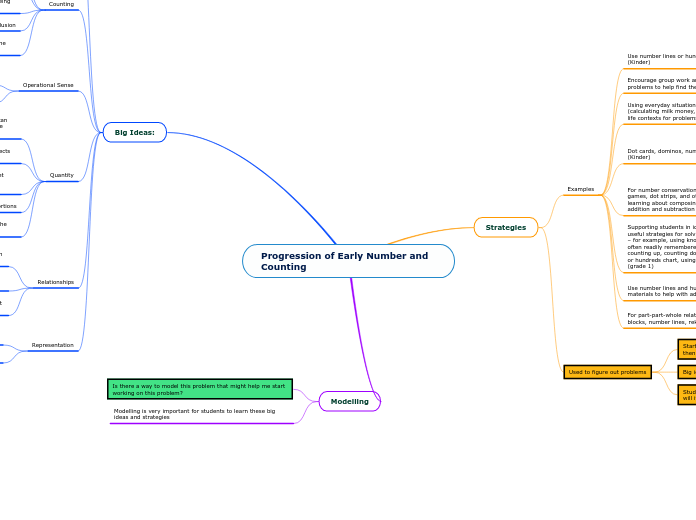
Strategies
Examples
Use number lines or hundreds carpet for rote counting (Kinder)
Encourage group work and drawing representations of math problems to help find the solution (grade 1 and Kinder)
Using everyday situations as contexts for problems (calculating milk money, taking attendance) and/or using real-life contexts for problems (grade 1)
Dot cards, dominos, number of fingers, and dice for subitizing (Kinder)
Composing and Decomposing numbers is a strategy for subitizing (Kinder)
Subitizing is a good way to start learning estimation skills (Kinder)
For number conservation, use things like linking cubes, games, dot strips, and other concrete materials to start learning about composing and decomposing numbers and addition and subtraction (Kinder)
Supporting students in identifying, developing, and describing useful strategies for solving addition and subtraction problems – for example, using known facts, using doubles (which are often readily remembered), making tens, using compensation, counting up, counting down, using a number line
or hundreds chart, using the commutative property of addition (grade 1)
Use number lines and hundreds charts along with concrete materials to help with addition and subtraction (grade 1)
Concrete materials (i.e. beans) can be helpful for rote counting, one-to-one correspondence and cardinality (Kinder and grade 1)
For part-part-whole relationships, use things like counters, blocks, number lines, rekenreks (grade 1)
Used to figure out problems
Start with strategies that are less efficient gets refined and then are more efficient
Big ideas can help students create new strategies
Students will be surprised that the strategy works so they ask- will it work all the time?
Big Ideas:
Cognitive reorganizing when looking at big ideas
Like Piaget's development of structures
Brain needs to develop new synapses- similar to when mathematicians figure these big ideas out
Counting
Stable Order - the idea that the counting sequence stays consistent
Rote Counting
One-to-One Correspondence- the idea that each object being counted must be given one count and only one count
Hierarchical Inclusion
Movement is Magnitude- the idea that as one moves up the counting sequence, the quantity increases or vice versa
Operational Sense
Subitizing- recognize small quantities without having to count each of the objects
Rational Numbers
Quantity
Order Irrelevance- the idea that the counting of objects can begin with any object in a set and the total will still be the same
Cardinality- the idea that the last count of a group of objects represents the total number of objects in the group
Conservation of Number - the idea that the count for a set group of objects stays the same no matter whether the objects are spread out or are close together
Proportions
Movement is Magnitude- the idea that as one moves up the counting sequence, the quantity increases or vice versa
Relationships
Part-Part Whole- the ideas that quantities represented by such numbers are made up of different parts
Unitizing- the idea that in the base ten system, objects are grouped into tens once the count exceeds 9
Anchors of 5 and 10- students develop the understanding that numbers such as 2 can be thought of in relation to 5
Representation
Abstraction- the idea that a quantity can be represented by different things
Decomposition and Composition of Numbers
Modelling
Is there a way to model this problem that might help me start working on this problem?
Modelling is very important for students to learn these big ideas and strategies