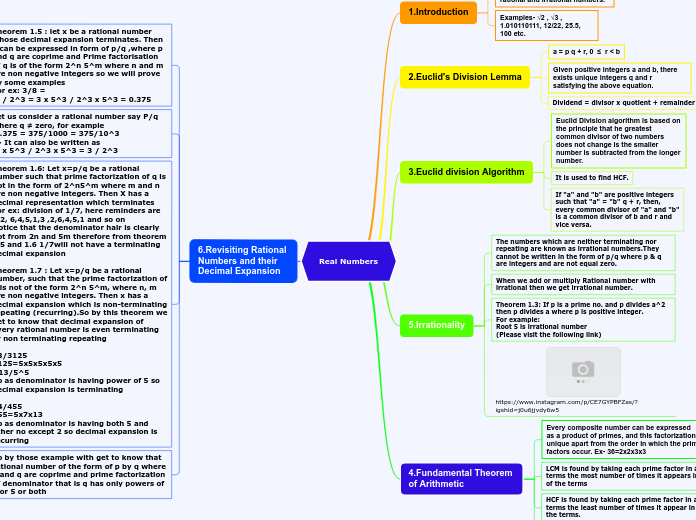
Real Numbers

Real number consist of both rational and irrational numbers.

Examples- √2 , √3 , 1.010110111, 12/22, 25.5, 100 etc.

a = p q + r, 0 ≤ r < b

Given positive integers a and b, there exists unique integers q and r satisfying the above equation.

Dividend = divisor x quotient + remainder

Euclid Division algorithm is based on the principle that he greatest common divisor of two numbers does not change is the smaller number is subtracted from the longer number.

It is used to find HCF.

If "a" and "b" are positive integers
such that "a" = "b" q + r, then,
every common divisor of "a" and "b"
is a common divisor of b and r and
vice versa.

The numbers which are neither terminating nor repeating are known as irrational numbers.They cannot be written in the form of p/q where p & q are integers and are not equal zero.

When we add or multiply Rational number with irrational then we get irrational number.

Theorem 1.3: If p is a prime no. and p divides a^2 then p divides a where p is positive integer.
For example:
Root 5 is irrational number
(Please visit the following link)

Every composite number can be expressed
as a product of primes, and this factorization is unique apart from the order in which the prime factors occur. Ex- 36=2x2x3x3

LCM is found by taking each prime factor in all the terms the most number of times it appears in any of the terms

HCF is found by taking each prime factor in all the terms the least number of times it appear in any of the terms.

HCF(a,b) x LCM(a,b) = a x b

Theorem 1.5 : let x be a rational number whose decimal expansion terminates. Then x can be expressed in form of p/q ,where p and q are coprime and Prime factorisation of q is of the form 2^n 5^m where n and m are non negative integers so we will prove by some examples
For ex: 3/8 =
3 / 2^3 = 3 x 5^3 / 2^3 x 5^3 = 0.375

Let us consider a rational number say P/q where q ≠ zero, for example
0.375 = 375/1000 = 375/10^3
-> It can also be written as
3 x 5^3 / 2^3 x 5^3 = 3 / 2^3

Theorem 1.6: Let x=p/q be a rational number such that prime factorization of q is not in the form of 2^n5^m where m and n are non negative integers. Then X has a decimal representation which terminates
For ex: division of 1/7, here reminders are 3,2, 6,4,5,1,3 ,2,6,4,5,1 and so on
Notice that the denominator hair is clearly not from 2n and 5m therefore from theorem 1.5 and 1.6 1/7will not have a terminating decimal expansion

Theorem 1.7 : Let x=p/q be a rational number, such that the prime factorization of q is not of the form 2^n 5^m, where n, m are non negative integers. Then x has a decimal expansion which is non-terminating repeating (recurring).So by this theorem we get to know that decimal expansion of every rational number is even terminating or non terminating repeating

13/3125
3125=5x5x5x5x5
=13/5^5
So as denominator is having power of 5 so decimal expansion is terminating

64/455
455=5x7x13
So as denominator is having both 5 and other no except 2 so decimal expansion is recurring

So by those example with get to know that rational number of the form of p by q where p and q are coprime and prime factorization of denominator that is q has only powers of 2 or 5 or both