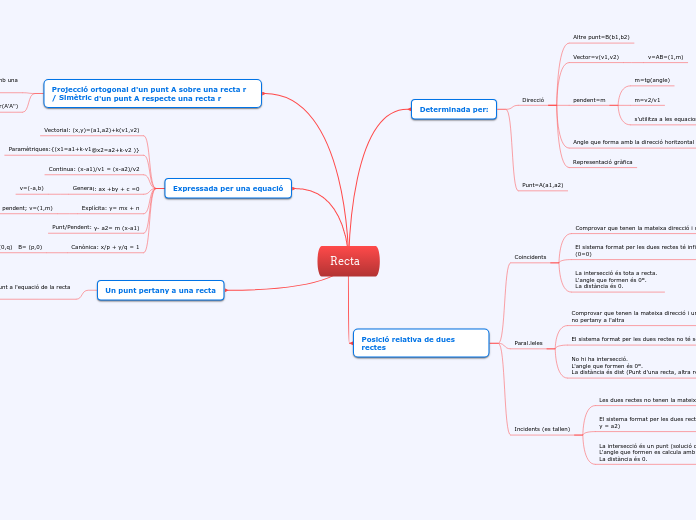
Recta

Direcció

Altre punt=B(b1,b2)

Vector=v(v1,v2)

v=AB=(1,m)

pendent=m

m=tg(angle)

m=v2/v1

s'utilitza a les equacions explícita i punt/pendent

Angle que forma amb la direcció horitzontal

Representació gràfica

Punt=A(a1,a2)

Coincidents

Comprovar que tenen la mateixa direcció i un punt en comú

El sistema format per les dues rectes té infinites solucions (0=0)

La intersecció és tota a recta. L'angle que formen és 0º. La distància és 0.

Paral.leles

Comprovar que tenen la mateixa direcció i un punt d'una recta no pertany a l'altra

El sistema format per les dues rectes no té solució (0=5)

No hi ha intersecció. L'angle que formen és 0º. La distància és dist (Punt d'una recta, altra recta).

Incidents (es tallen)

Les dues rectes no tenen la mateixa direcció

El sistema format per les dues rectes té solució única ( x=a1; y = a2)

La intersecció és un punt (solució del sistema). L'angle que formen es calcula amb el producte escalar. La distància és 0.

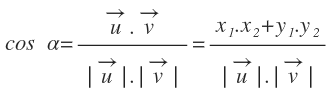
Projecció ortogonal A': Intersecció de la recta donada amb una recta ortogonal que passi pel punt

Simètric A'': Punt que verifica vector(AA') =vector(A'A'')

Vectorial: (x,y)=(a1,a2)+k(v1,v2)

Paramètriques:{(x1=a1+k·v1@x2=a2+k·v2 )}

Continua: (x-a1)/v1 = (x-a2)/v2

General: ax +by + c =0

v=(-a,b)

Explícita: y= mx + n

m= pendent; v=(1,m)

Punt/Pendent: y- a2= m (x-a1)

Canònica: x/p + y/q = 1

A=(0,q) B= (p,0)

Si al substituir les coordenades del punt a l'equació de la recta la igualtat és certa