Temas 9-10, Funciones
Concepto de función
Una función es la relación entre dos magnitudes, x e y, de forma que a cada valor de x de la primera magnitud le corresponde un único valor y de la segunda. Así, x se denomina variable independiente e y es la variable dependiente

Continuidad y puntos de corte con los ejes
Continuidad
Una función es continua si su gráfica puede dibujarse de un solo trazo, los puntos donde se irrumpe la gráfica se llaman puntos de discontinuidad de la función

Evitables
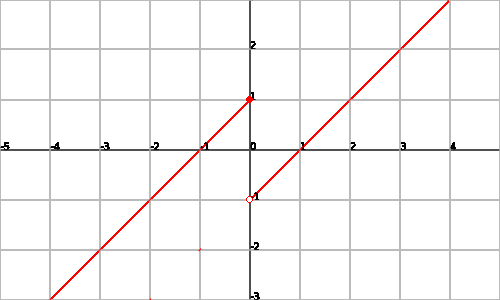
Inevitables de salto finito

Inevitables de salto infinito
Puntos de corte con los ejes
En el eje x
(a,0), el valor de la a se calcula resolviendo f(x)=0
En el eje y
(0,b), el valor de b se obtiene hallando f(0)
Simetría y periodicidad
Simetría
Funciones pares
f(-x)=f(x)

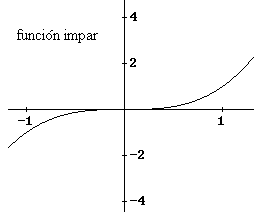
Funciones impares
f(-x)=-f(x)
Periodicidad
Una función es periódica si los valores de y se repiten cada cierto intervalo
La amplitud se llama período

Funciones definidas a trozos

Dominio y recorrido
Dominio
Todos los valores que toma la variable independiente
Recorrido
Conjunto de valores que toma la variable dependiente
Crecimiento y decrecimiento
Si f(x1)<f(x2) es creciente en el intervalo (a,b)
Si f(x1)>f(x2) es decreciente en el intervalo (a,b)
Si f(x1)=f(x2) es constante en el intervalo (a,b)
Una función tiene un máximo cuando en x=a la función pasa de ser creciente a decreciente
Una función tiene un mínimo si cuando en x=a la función pasa de ser decreciente a creciente
Funciones polinómicas de primer grado
Una función polinómica es aquella cuya expresión algebraica es un polinomio
Son de la forma y=mx+n
Tipos

Lineal
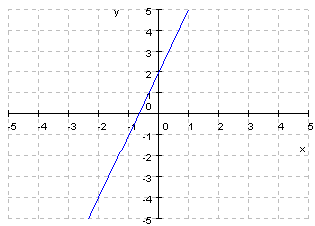
Proporcionalidad directa

Constante
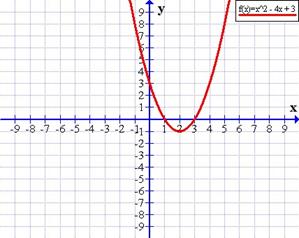
Funciones polinómicas de segundo grado
Son parábolas, cuyas ramas son una creciente y una decreciente
Tienen
Vértice
Es el punto en el que la función pasa de ser creciente a decreciente, o a la inversa
Eje de simetría
Recta que pasa por el vértice, paralela al eje Y y divide a la parábola en dos partes simétricas
Sentido
Si a<0 las ramas van hacia abajo y si a>0 hacia arriba
Tipos
y=a(x·x)
Vértice en el (0,0) y eje de simetría = eje Y

y=a(x·x)+c
Vértice=(0,c) y eje de simetría es el eje Y
=+a.x2+++c+,+a+%3E+0+,+c+%3E+0.jpg)
y=a(x·x) +bx
Vértice=(-b/2a, -(b·b)/4a) y eje de simetría es -b/2a
=+a.x2+++b.x+,+a+%3C+0+,+b+%3E+0.jpg)
y=a(x·x)+bx+c
Vértice=(-b/2a, -(b·b)+4ac/4a) y eje de simetría es -b/2a