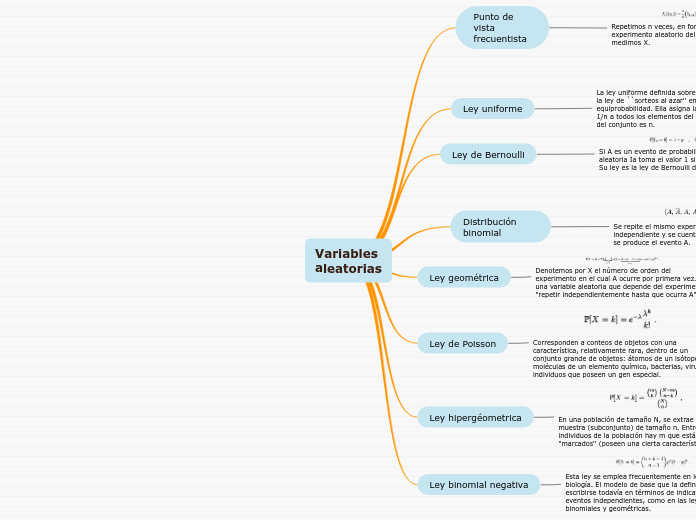
Variables
aleatorias
Punto de vista frecuentista

Repetimos n veces, en forma independiente, el experimento aleatorio del cual como resultado medimos X.
Ley uniforme
La ley uniforme definida sobre un conjunto finito es la ley de ``sorteos al azar'' en este conjunto o equiprobabilidad. Ella asigna la misma probabilidad 1/n a todos los elementos del conjunto, si el cardinal del conjunto es n.
Ley de Bernoulli

Si A es un evento de probabilidad p, la variable aleatoria Ia toma el valor 1 si A se realiza y 0 si no. Su ley es la ley de Bernoulli de parámetro p.
Distribución binomial

Se repite el mismo experimento n veces en forma independiente y se cuenta el número de veces que se produce el evento A.
Ley geométrica

Denotemos por X el número de orden del experimento en el cual A ocurre por primera vez. Es una variable aleatoria que depende del experimento:
"repetir independientemente hasta que ocurra A".
Ley de Poisson

Corresponden a conteos de objetos con una característica, relativamente rara, dentro de un conjunto grande de objetos: átomos de un isótopo, moléculas de un elemento químico, bacterias, virus, individuos que poseen un gen especial.
Ley hipergéometrica

En una población de tamaño N, se extrae al azar una muestra (subconjunto) de tamaño n. Entre los N individuos de la población hay m que están "marcados'' (poseen una cierta característica).
Ley binomial negativa

Esta ley se emplea frecuentemente en los conteos en biología. El modelo de base que la define puede escribirse todavía en términos de indicatrices de eventos independientes, como en las leyes binomiales y geométricas.