por Fermín Enrique Estrada Sánchez 7 anos atrás
891
Métodos simplex, sensibilidad, dual y posoptimalidad - Taha (3 y 4)
por Fermín Enrique Estrada Sánchez 7 anos atrás
891

Mais informações
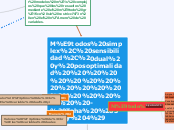
Además, la solución actual no satisface la nueva restricción, y debe determinarse una nueva solución mediante el método simplex dual.