Organigrama

Mais informações

Funciones del Lenguaje Se entiende por las funciones del lenguaje a los distintos cometidos con que el ser humano emplea el lenguaje, es decir, los propósitos comunicativos con los que utiliza esa herramienta cognitiva y abstracta.

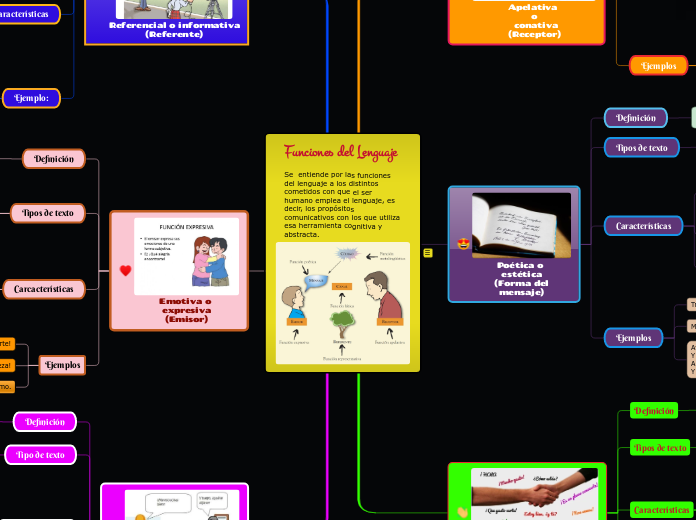
por DAYANA LIZBETH CAICEDO ESPINOSA

DILEMA MORAL

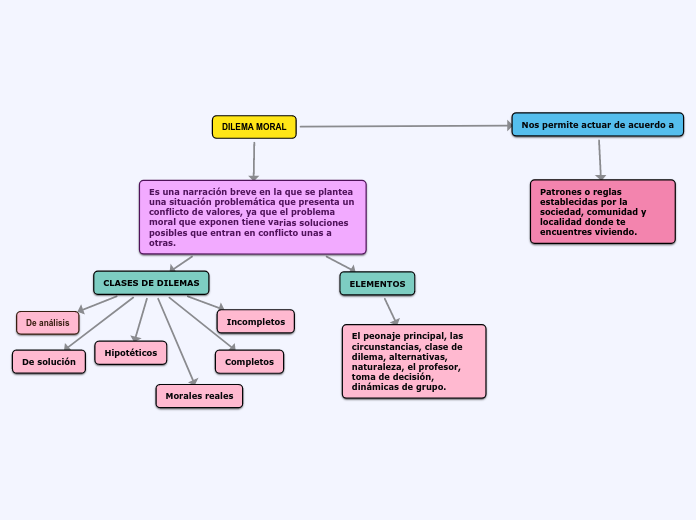
por Maria Celeste Dager

LA BASE D ELA CONDUCTA SOCIAL

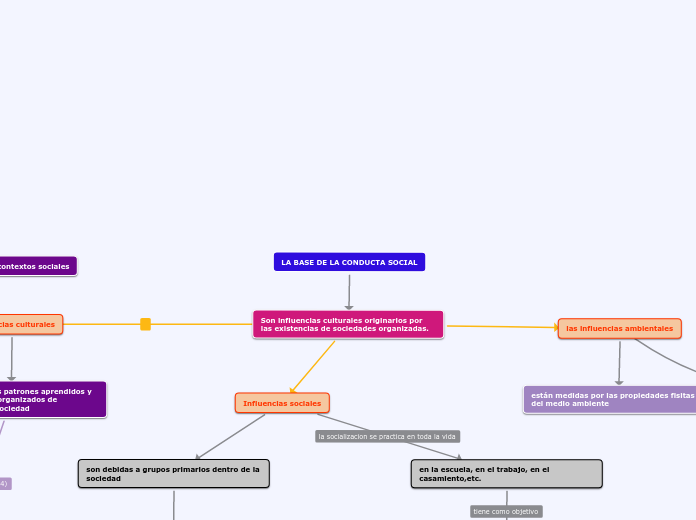
por milagros garcia

Personalidad: temperamento y carácter

por Luis Portes

Limites Infinitos

Topic principal

Subtema

Se dice que existe límite infinito cuando la función f(x) llega a valores que crecen continuamente, es decir que se puede hacer la función tan grande como queramos. Se dice que f(x) diverge a infinito.

Tipos de limites

Para cualquier valor de la función f(a) positivo, negativo, por muy grande que sea en su valor absoluto, (siendo a < 0), siempre encontraremos otro f(b) tal que si b < a entonces f(b) < f(a).

Límite = -∞ cuando x → +∞

Para cualquier valor de la función f(a) negativo, por muy grande que sea en su valor absoluto, (siendo a > 0), siempre encontraremos otro f(b) tal que si b > a entonces f(b) < f(a).

Límite = +∞ cuando x → -∞

Para cualquier valor de la función f(a) positivo, por muy grande que sea, (siendo a < 0), siempre encontraremos otro f(b) tal que si b < a entonces f(b) > f(a).

Límite = +∞ cuando x → +∞

Para cualquier valor de la función f(a) positivo, por muy grande que sea, (siendo a > 0), siempre encontraremos otro f(b) tal que si b > a entonces f(b) > f(a).

Límite = -∞ cuando x → a

Para cualquier valor de la función f(a) existe un entorno pequeño alrededor de a en el que se cumple que f(x) < f(a).

Límite = +∞ cuando x → a

Para cualquier valor de la función f(a) existe un entorno pequeño alrededor de a en el que se cumple que f(x) > f(a).

Límite = -∞ cuando x → -∞