por LAURA VALENTINA VALIENTE RODRIGUEZ 2 anos atrás
274
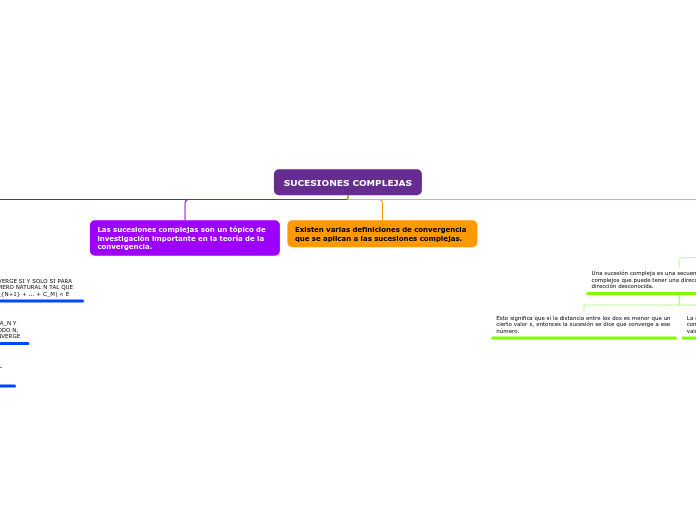
SUCESIONES COMPLEJAS
por LAURA VALENTINA VALIENTE RODRIGUEZ 2 anos atrás
274

Mais informações
DADA UNA SERIE COMPLEJA Σ C_N, SI EXISTE UN LÍMITE L TAL QUE LIM |C_{N+1}/C_N| = L, ENTONCES LA SERIE CONVERGE SI L 1
SI Σ A_N Y Σ B_N SON DOS SERIES COMPLEJAS CON A_N Y B_N NÚMEROS COMPLEJOS, Y |A_N| ≤ |B_N| PARA TODO N, ENTONCES SI Σ B_N CONVERGE, Σ A_N TAMBIÉN CONVERGE
UNA SERIE COMPLEJA Σ C_N CONVERGE SI Y SOLO SI PARA CUALQUIER Ε > 0, EXISTE UN NÚMERO NATURAL N TAL QUE PARA TODO M > N ≥ N, |C_N + C_{N+1} + ... + C_M| < Ε