Геометрія 9-ий клас
Площа круга
Площа круга обчислюється за формулами:S=ПR2,або S=Пd2/4,де R – радіус круга, d – його діаметр.
Круговий сектор
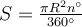
За цією формулою можна обчислити S сектора,де n° – градусна міра дуги сектора.
Круговим сектором називається частина круга, яка лежить усередині відповідного центрального кута.
Кругові кільця
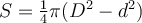
Круговим кільцем називається частина площини, обмежена двома концентричними колами.
Площа кругового кільця дорівнює різниці площ зовнішнього і внутрішнього кругів,де D – діаметр зовнішнього круга, d – діаметр внутрішнього круга.
Круговий сегмент
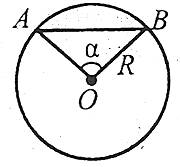
Круговим сегментом називається спільна частина круга і півплощини. Якщо круг перетнути прямою, то він ділиться на два кругових сегменти.
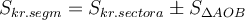
Площу кругового сегмента можна обчислити даною формулою,причому при α<180° беремо знак «-», а при α>180° – знак «+».
Правильні многокутники
Основні теоретичні відомості:
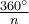
а зовнішній
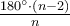
Кожний внутрішній кут правильного n-кутника дорівнює
Апофемою правильного многокутника називають перпендикуляр, проведений із центра правильного многокутника на його сторони.
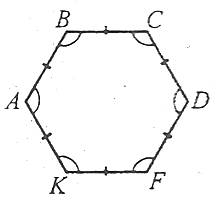
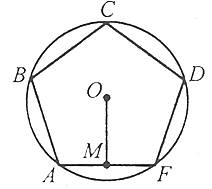
Опуклий многокутник називають правильним, якщо в нього всі сторони і всі кути рівні.
Вписані та описані многокутники:
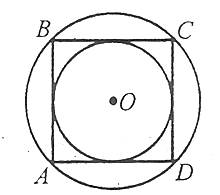
Кожний правильний многокутник можна вписати в деяке коло і описати навколо кола. Вписані і описані кола правильного многокутника мають один і той же центр, який називають центром правильного многокутника.
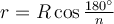
Радіуси r i R відповідно вписаного і описаного кіл правильного n-кутника пов’язані між собою співвідношенням:
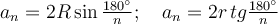
Співвідношення між стороною an правильного n-кутника та радіусами описаного R і вписаного r кіл виражається формулами:

для правильного трикутника:
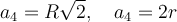
для правильного чотирикутника:
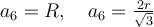
для правильного шестикутника:
Довжина кола
Довжина С кола обчислюється за формулою: С=2ПR,або С=Пd
Відношення довжин двох кіл дорівнює відношенню їх радіусів:С1/C2=R1/R2
Довжина дуги
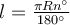
За допомогою цієї формули можна обчислити довжину дуги кола радіуса.де l – довжина дуги; n° – градусна міра дуги.
Число П
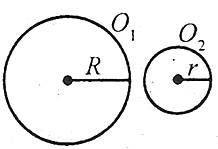
Відношення довжини кола до його діаметра не залежить від кола, тобто воно одне й те ж для будь-яких кіл.Це відношення прийнято позначати буквою П:С1/2R=C2/2r=П,П=3,1415926