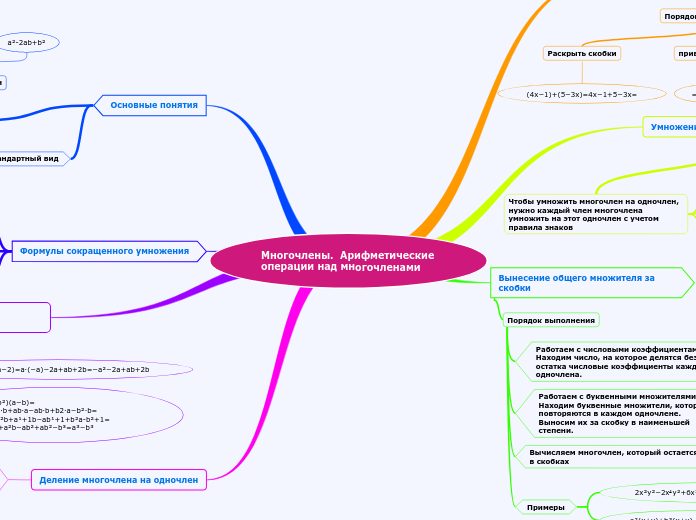
Многочлены. Арифметические операции над многочленами
Сложение и вычитание многочленов
Порядок выполнения
Раскрыть скобки
(4x−1)+(5−3x)=4x−1+5−3x=
привести подобные
=4x−3x−1+5=
Выполнить сложение(вычитание)
=x+4
Умножение многочлена на одночлен
Чтобы умножить многочлен на одночлен, нужно каждый член многочлена умножить на этот одночлен с учетом правила знаков
6a(3a−b)=6a·3a−6ab=18a¹+1−6ab=18a²−6ab
−4a(−a+b)=(−4a)·(−a)−4ab=4a·a-4ab= =4a¹+1−4ab=4a²−4ab
xyz(x^2+2y²−3z²)=xyz·x²+xyz·2y²−xyz·3z²= x²+1yz+2xy²+1z-3xyz²+1 =x³yz+2xy³z−3xyz³
Вынесение общего множителя за скобки
Порядок выполнения
Работаем с числовыми коэффициентами. Находим число, на которое делятся без остатка числовые коэффициенты каждого одночлена.
Работаем с буквенными множителями. Находим буквенные множители, которые повторяются в каждом одночлене. Выносим их за скобку в наименьшей степени.
Вычисляем многочлен, который остается в скобках
Примеры
2x²y²−2x⁴y²+6x³y³=2x²y²(1−x²+3xy)
a²(x+y)+b³(x+y)=(x+y)(a²+b³)
Основные понятия
многочлен
Двучлен
ab-3c
Трёхчлен
a⁴+6a²b+9b²
a²-2ab+b²
стандартный вид
3a²x+3ax²+5a⁴-3ax²-8a²x-10a⁴=-5a²x-5a⁴
m²-2mn+n²-m²-2mn-n²=-4mn
Формулы сокращенного умножения
Разность квадратов
a²-b²=(a+b)(a-b)
Квадрат разности
(a-b)²=a²-2ab+b²
Квадрат суммы
(a+b)²=a²+2ab+b²
Умножение многочлена на многочлен
каждый одночлен первого многочлена умножить на каждый одночлен второго многочлена. Полученные произведения сложить (то есть записать друг за другом с учетом знаков полученных при умножении)
(a−b)(−a−2)=a·(−a)−2a+ab+2b=−a²−2a+ab+2b
(a²+ab+b²)(a−b)= =a²·a−a²·b+ab·a−ab·b+b2·a−b²·b= =a²+1−a²b+a¹+1b−ab¹+1+b²a-b²+1= =a³−a²b+a²b−ab²+ab²−b³=a³−b³
Деление многочлена на одночлен
разделить отдельно каждый одночлен исходного многочлена на одночлен по правилу деления одночленов. Сложить полученные результаты деления одночленов (то есть записать друг за другом с учетом правила знаков)