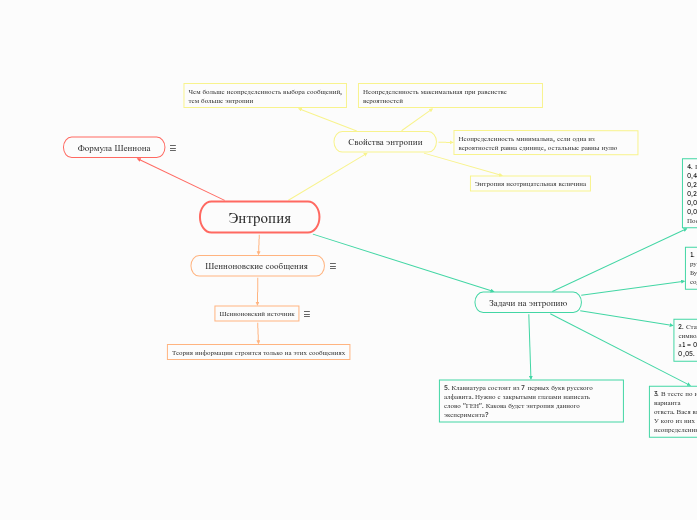
Энтропия

Формула Шеннона

H=\sum _{i=1}^NP_i\cdot \log _2P_i

Шенноновские сообщения

Сообщения, в которых вероятность каждого знака не меняется со временем

Шенноновский источник

Отправитель Шенноновских сообщений

Теория информации строится только на этих сообщениях

Свойства энтропии

Чем больше неопределенность выбора сообщений,
тем больше энтропии

Неопределенность максимальная при равенстве вероятностей

Неопределенность минимальна, если одна из вероятностей равна единице, остальные равны нулю

Энтропия неотрицательная величина

Задачи на энтропию

1. В 1 классе дети сдают тест на знание букв
русского алфавита, вытягивая карточки букв из мешочка.
Буквы Ъ Ы Ь в мешочек не положили. Какую энтропию содержит данный тест?

2. Статистика распределения вероятностей появления
символов на выходе источника:
а1 = 0,25; а2 = 0,05; а3 = 0,2; а4 = 0,25; а5 = 0,2; а6 = 0,05. Найти энтропию системы.

3. В тесте по истории 10 вопросов, в каждом по 3 варианта
ответа. Вася выучил 5 вопросов, а Катя только 2 вопроса. У кого из них решение теста будет более неопределенным?

4. Правила выигрыша в лотерею следующие:
0,47 - ничего
0,256 - купон на 1000 р. в продуктовый магазин
0,242 - промокод
0,02 - футболка
0,004 - телефон
Посчитать энтропию лотереи.

5. Клавиатура состоит из 7 первых букв русского
алфавита. Нужно с закрытыми глазами написать
слово "ГЕН". Какова будет энтропия данного эксперимента?