Actividad 2 - Enseñanza y aprendizaje de las matemáticas en niños y niñas de educación inicial
Generalización completitiva: Los educadores pueden presentar situaciones donde los estudiantes deben integrar conocimientos previos con nueva información para resolver problemas más complejos, promoviendo así una comprensión más profunda de los conceptos matemáticos. (Porras Corredor, 2011, pág. 110)
Instrumentos comparativos
Correspondencias
Unidireccionales
uno a uno, uno a varios, varios a uno.
Bidireccionales
Uno a uno
Inclusivas
Parte - todo
Exclusivas
No hay elementos comunes
¿Cuáles procesos mentales se activan y cómo se va dando forma a los conceptos cuando un individuo se ve enfrentado a resolver un asunto relativo a las matemáticas?

Percepción, identificar los datos principales del problema

Atención, crear en la mente una imagen del problema

Generalización, recobrar información almacenada en la memoria a largo plazo útil para resolver el problema.

Memoria, plantear diferentes medidas posibles al problema

Razonamiento, elegir la estrategia más probable para llegar a la respuesta correcta.
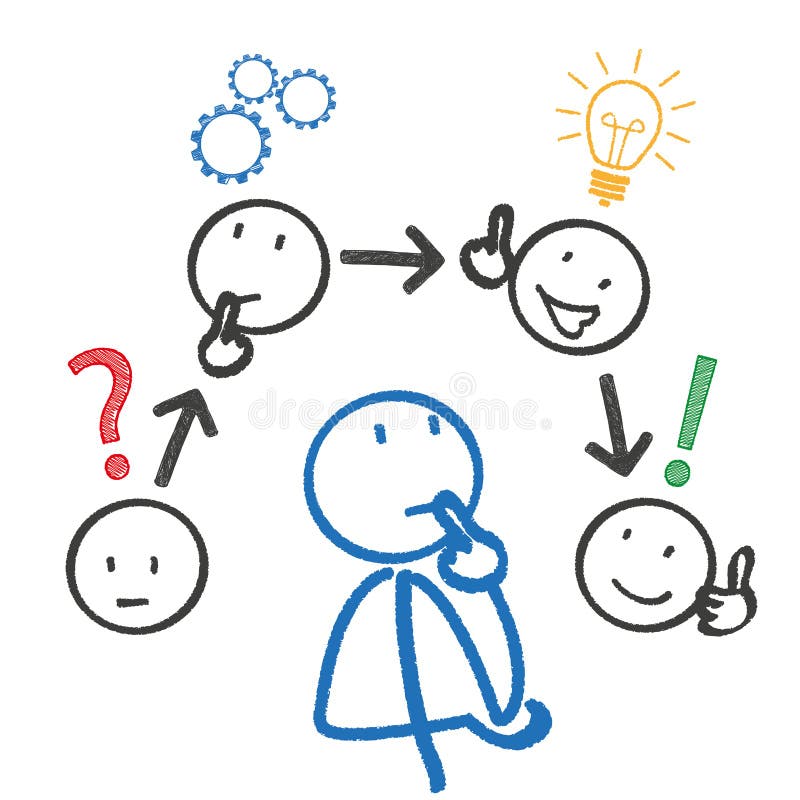
Resolución de problemas, realizar las acciones previstas para solucionar la situación.
Determinar si se está progresando hacia la respuesta adecuada y efectuar modificaciones en caso de ser requerido.
Verificar si la respuesta obtenida es precisa.
Metacognición, pensar en la táctica empleada y en posibles mejoras para el mañana.
Topic principal
Mecanismo intra-inter-trans: Este mecanismo puede ser aplicado al animar a los estudiantes a reflexionar sobre su propio pensamiento (intra), compararlo con el de sus compañeros (inter) y luego aplicar este conocimiento a situaciones nuevas o más abstractas (trans). (Porras Corredor, 2011, págs. 119,125)
Seriaciones
Continuas
ordenamiento de elementos con base en una magnitud.
Discontinuas
ordenamiento de elementos con base en categorías.
Generalización constructiva: Se puede fomentar en los estudiantes a través de actividades que les permitan identificar patrones y relaciones en conjuntos de datos o problemas matemáticos, llevándolos a formular sus propias generalizaciones. (Porras Corredor, 2011, pág. 110)
Operaciones matemáticas
Sumas
combinación de cantidades.
Restas
separación de cantidades.
Multiplicaciones
repetición de cantidades.
Divisiones
reparto de cantidades.
Instrumentos transformantes
Subtópico
Operaciones lógicas
Negación
Invierte el valor de verdad de una proposición.
Conjunción
Combina dos proposiciones en una sola que es verdadera solo si ambas son verdaderas
Disyunción
Ordena dos proposiciones en una sola que es verdadera si al menos una de ellas es verdadera.
Implicación
Establece una relación de causa-efecto entre dos proposiciones.
Equivalencia
Indica que dos proposiciones tienen el mismo valor de verdad.