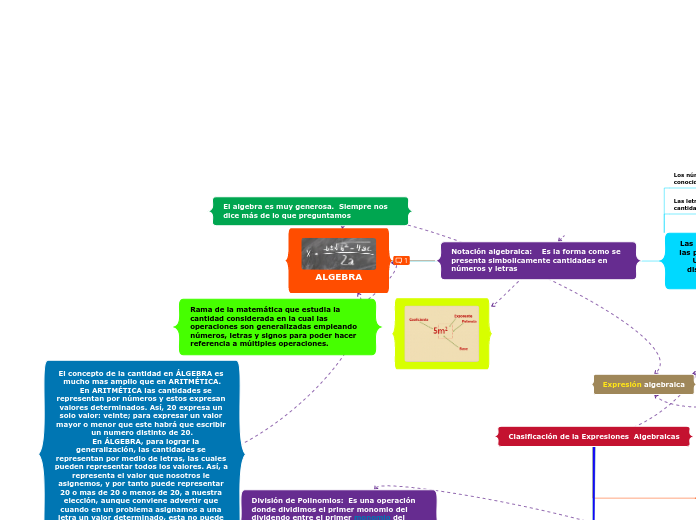
ALGEBRA

Notación algebraica: Es la forma como se presenta simbolicamente cantidades en números y letras

Las cantidades conocidas se expresan por las primeras letras del alfabeto: a,b,c,d... Una misma letra puede representar distintos valores diferencian dolos por medio de comillas.

Los números se emplean para representar cantidades conocidas y determinadas.

Las letras se emplean para representar toda clase de cantidades, ya terminadas

El algebra es muy generosa. Siempre nos dice más de lo que preguntamos

El concepto de la cantidad en ÁLGEBRA es mucho mas amplio que en ARITMÉTICA.
En ARITMÉTICA las cantidades se representan por números y estos expresan valores determinados. Así, 20 expresa un solo valor: veinte; para expresar un valor mayor o menor que este habrá que escribir un numero distinto de 20.
En ÁLGEBRA, para lograr la generalización, las cantidades se representan por medio de letras, las cuales pueden representar todos los valores. Así, a representa el valor que nosotros le asignemos, y por tanto puede representar 20 o mas de 20 o menos de 20, a nuestra elección, aunque conviene advertir que cuando en un problema asignamos a una letra un valor determinado, esta no puede representar, en el mismo problema, otro valor distinto del que le hemos asignado.

Conjunto de números y de símbolos ligados entre sí por los signos de las operaciones del álgebra y que no contiene más funciones que aquéllas que pueden calcularse con las operaciones del álgebra. Una expresión algebraica puede tener uno o varios términos separada por signos positivos + o negativos -

Si tenemos la expresión 3X=12, el valor de la incógnita X para la cual se cumple la expresión es 4, ya que 3 por 4 es igual a 12

Rama de la matemática que estudia la cantidad considerada en la cual las operaciones son generalizadas empleando números, letras y signos para poder hacer referencia a múltiples operaciones.

Expresión algebraica

Clasificación de la Expresiones Algebraicas

Monomio: Expresión algebraica que consta de un solo término. Las únicas operaciones matemáticas que aparecen son la multiplicación y la potencia de exponente natural, es decir, de exponentes con números positivos. Un ejemplo sería:

2x²

2x2y3z.

Polimonios: Expresión algebraica que consta de más de un término. Ejemplo: x+y+z

ab³ + 5a² b⁷ m – 35 abx⁵

Binomios: Es un polinomio que consta de dos términos. Ejemplo: a⁴ b⁵ + 3 a² b² c⁷

Términos Semejantes: Dos o más términos son semejantes cuando tienen la misma parte literal, o sea, cuando tienen letras iguales afectadas de iguales exponentes

Reducción de Terminos Semejantes: Convertir en un solo términi dos o más términos semejantes

Clases de Polinomios

Trinomio: Es un polnomio que consta de tres términos. Ejemplo: ab³ + 5a² b⁷ m – 35 abx⁵

Valor númerico: Resultado al sustituir las letras por valores númericos dados y efectuar despúes las operaciones indicadas

Suma o Adición: Es una operación que tiene por objeto reunir dos o más expresiones algebraicas (sumandos) en una sola expresión algebraica (suma) En Aritmética la suma siempre significa aumento,pero en algebra puede ser aumento o disminución

con sus propios signos y se reducen los términos semejantes si los hay

SUMA DE MONOMIOS:El orden de los sumandos no altera la suma

Suma de Polinomios:: lA SUMA DE POLINOMIOS PUEDE INDICARSE INCLUYENDO LOS SUMANDOS DENTRO DE LOS PARENTESIS

El valor númerico de los sumandos y de la suma para los mismos valores, que fijamos nosotros, de las letras. Si la operación está correcta, la suma algebraica de los valores númericos de los sumandos debe ser igual al valor númerico de la suma.

Resta o Sustracción:La suma del sustraendo y la diferencia tiene que ser el minuendo, escribiendo el minuendo con sus propios signos y el sustraendo con los signos cambiados. La resta implica disminución, mientras que la algebraica tiene un carácter más general, significa disminución o aumento

RESTA DE MONOMIOS: La resta de monomios es muy parecida a la suma, sólo que hay que cambiar los números del sustraendo por su simétrico y se resuelve aplicando las reglas de la suma.

Ejemplo: si tenemos (8x) – (6x) =

a) Se convierte la resta en suma cambiando el sustraendo por su simétrico.



(8x) + (-6x) =



b) Se resuelve aplicando las reglas de la suma.



(8x) + (-6x) = (8-6) x = +2x

Resta de Polinomios Restar del minuendo cada uno de los términos del sustraendo

Multiplicación: Multiplicación de polinomios
Se multiplica cada monomio del primer polinomio por todos los elementos del. segundo polinomio. ...
Se suman los monomios del mismo grado (suma de términos semejantes) y obtenemos: ...

El polinomio obtenido es otro polinomio cuyo grado es la suma de los grados de los polinomios.

El orden de los factores no altera el producto

Los factores de un producto pueden agruparse de cualquier modo.

Ley de los Signos

La ley se basa en lo siguiente: si los signos son iguales el resultado debe ser positivo. En cambio si los signos son diferentes el resultado será negativo. En otras palabras podría decirse signos iguales se suman, signos diferentes se restan.

Ley de los Exponentes

Multiplicar expresiones exponenciales de la misma base, se conserva la base común y se suman los exponentes.

Ley de los Coeficientes

El coeficiente del producto de dos o más términos es igual al producto de los coeficientes de los términos.

La multiplicación de monomios es otro monomio que tiene por coeficiente el producto de los coeficientes y cuya parte literal se obtiene multiplicando las potencias que tengan la misma base, es decir, sumando los exponentes.

Multiplicación de Monomios

División de Polinomios: Es una operación donde dividimos el primer monomio del dividendo entre el primer monomio del divisor. Volvemos a dividir el primer monomio del dividendo entre el primer monomio del divisor. Y el resultado lo multiplicamos por el divisor y lo restamos al dividendo. Procedemos igual que antes.

Factorizar una expresión algebraica, es un proceso que consiste en expresar una suma o diferencia de términos como el producto de dos o más factores. Existen diferentes métodos para factorizar una expresión algebraica.

factorizar un polinomio con coeficientes en un campo dado o en los números enteros en factores irreducibles con coeficientes en el mismo dominio.

PRODUCTOS NOTABLES:

Son simplemente multiplicaciones especiales entre expresiones algebraicas, que por sus características destacan de las demás multiplicaciones. Las características que hacen que un producto sea notable, es que se cumplen ciertas reglas, tal que el resultado puede ser obtenido mediante una simple inspección, sin la necesidad de verificar o realizar la multiplicación paso a paso.

Regla del cuadrado de la suma de dos cantidades
El cuadrado de la suma de dos cantidades es igual al cuadrado de la primera cantidad, más dos veces la primera cantidad por la segunda, más el cuadrado de la segunda cantidad. Ejemplo: (a+b)2= (a+b) (a+b)

PRODUCTO DE LA SUMA POR LA DIFERENCIA DE DOS CANTIDADES

suma por diferencia es igual a diferencia de cuadrados". ... Es decir, que el resultado de multiplicar la suma de dos números por su diferencia es el mismo que si restamos los cuadrados de ambos números.

CUBO DE UN BINOMIO: Un binomio al cubo (suma) es igual al cubo del primero, más el triple del cuadrado del primero por el segundo, más el triple del primero por el cuadrado del segundo, más el cubo del segundo.

PRODUCTO DE DOS BINOMIOS AL TÉRMINO COMÚN: El producto de dos binomios que tienen un término común, se obtiene sumando algebraicamente el cuadrado del término común, el producto de este término por la suma algebraica de los términos no comunes y el producto de estos dos últimos términos.