CAMPO GRAVITATORIO
Concepciones históricas-Movimiento de los planetas
Platón
Las estrellas se movían en torno a la Tierra con trayectorias circulares y los planetas se encuentran el cielo.
Aristóteles
Combatió la idea de una Tierra plana, propuso el modelos de los 4 elementos y supuso que los cuerpos celestes giraban alrededor de la Tierra en esferas concéntricas rotatorias.
Ptolomeo
Modelo Geocéntrico
Las estrellas están fijas en el
cielo y los planetas giran alrededor de la
Tierra en una circunferencia denominada epiciclo.
Aceptado por la Iglesia ya que situaba al Ser Humano como el centro de todo.
Tycho Brahe
Aportó datos sobre la órbita de Marte, que
más tarde iban a ser cruciales para la formulación de las leyes correctas del movimiento de los planetas por parte de Kepler y rebatió la Tª Geocéntrica.
Aristarco de Samos
Modelo Heliocéntrico
Sol como centro del
mundo, y no a la Tierra.
Distancia Sol Tierra +> Distancia Luna Tierra
Sol > Tierra
Nicolás Copérnico
Sol como centro del Universo, La Tierra tiene un movimiento triple en torno a su centro, un movimiento anual en torno al Sol, y un movimiento cónico de su eje de rotación.
Galileo Galilei
Confirmo el Modelo Heliocéntrico
Descubre los satélites de Júpiter, demostrando así que existen más movimientos circulares en el universo y observando las manchas solares, dedujo la rotación solar.
Johannes Kepler
Las órbitas de los planetas son elípticas
Edwin Hubble
El espacio entre las galaxias
aumenta y que el universo se expande, aunque esta expansión queda disminuida por la atracción gravitatoria mutua de los cuerpos celestes.
Leyes de Kepler
1 Ley de las órbitas
Las órbitas de todos los planetas son elípticas y el Sol está en uno de sus focos.
2 Ley de las áreas
Los vectores de posición de los planetas se desplazan por áreas iguales , y lo hacen en el mismo tiempo.
3 Ley de los periodos
Los periodos al cuadrado son igualas a los cubos de sus distancias medias al Sol.
T² = K · a3
Ley de Gravitación Universal
Newton llamó gravitación a la interacción que se produce entre la Tierra y el Sol, la Tierra y la Luna o el Sol y los planetas.
F =( -G m1 m2/ r2 ) Ur
m1 y m2 son las masas de los cuerpos que se están atrayendo , r la distancia que existe entre estos y G es la cte de gravitación universal, G=6,67·10-11 N·m2·kg-2
Campo
¿Qué es?
Es la perturbación que un cuerpo causa en el espacio que lo rodea por el hecho de tener masa. .
Magnitud que lo caracteriza
Depende de la posición y del tiempo
Puede ser
Escalar
Vectorial
Puede
Variar de un punto a otro
No variar
Intensidad de Campo
g = F/m
= (-GM/r2) Ur
Topic principal
Líneas de Campo
Se utilizan para representar gráficamente el Campo Gravitatorio.
Definen la trayectoria que seguirían los cuerpos si se dejaran libres en el campo gravitatorio.
Su densidad depende de su propio módulo
Satélite Geoestacionario
¿Qué es?
Satélite que se encuentra siempre sobre el mismo punto de la superficie de la tierra

Velocidad de Escape
Fuerza necesaria que tiene que tener un cohete para escapar de la atracción de la campo gravitatorio que le afecta.
v = √ 2GM / r
Velocidad Orbital de un Satélite
Periodo
T = 2πr / Vo
Vo = √ GM/r
Cuando un satélite se encuentra en órbita
alrededor de un planeta,
Actúa sobre el la Fuerza de Atracción Gravitatoria
Fg = G Mm / r2
Provoca que se mueva de forma circular
Energía Orbital de un Satélite
Es la energía mecánica que este tiene cuando se encuentra en órbita.
E mecánica = E cinética + E potencial
E = (m/2) Vo2 = (-G/2) Mm/r
Potencial Gravitatorio
Es la energía potencial que tendría la unidad de masa si se colocara en dicho punto.
Relación con la Energía Potencial
V = Ep/m` = -G m/r
Se mide en (J · kg-1)
Relación con el campo gravitatorio
g = dv/dr
Carácter Conservativo
Cuando el Trabajo (W o Tau) no depende del recorrido que realiza un cuerpo al moverse de un punto a otro.
Energía Potencial Gravitatoria
Ep = -G m1 m2/r
Se mide en Julios (J)
Es una función que no depende del camino recorrido, solo de los puntos final e inicial.
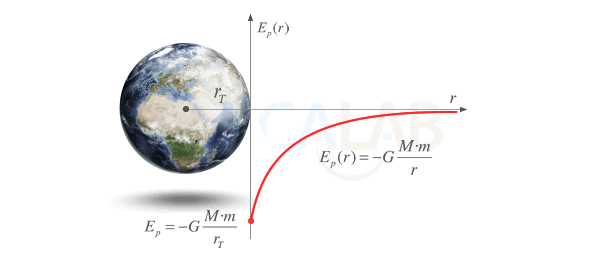
En el ∞ la Ep es 0, por lo que es mínima en valor absoluto pero también máxima
Sistema libre, las masas no van a atraerse entre ellas
Si la Ep no es igual a 0
Las masas si que interaccionarán entre sí y formarán un sistema ligado