Числовые характеристики случайной величины

r

Случайная величина - величина, которая в результате опыта может принимать то или иное значение, причём до завершения опыта неизвестно какое.Дискретная случайная величина - величина, которая может принимать отдельные, изолированные значения с определенными вероятностями

Дисперсия

Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания:

Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания:
c1

Для дискретной случайной величины X эта формула принимает вид:

Для дискретной случайной величины X эта формула принимает вид:

Для непрерывной случайной величины:

Для непрерывной случайной величины:

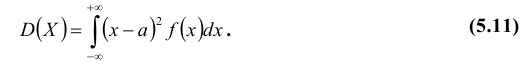
Свойства дисперсии:

Медиана

Медианой Ме(Х) непрерывной случайной величины Х называется такое ее значение, для которого вероятность того, что случайная величина Х примет значение, меньшее медианы или большее ее, одна и та же и равна 1/2.

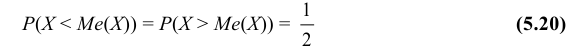
Медианой Ме(Х) непрерывной случайной величины Х называется такое ее значение, для которого вероятность того, что случайная ве
c1

Математические ожидание

Математическим ожиданием, или средним значением, M(X) дискретной случайной величины X называется сумма произведений всех ее значений на соответствующие им вероятности.

c1a

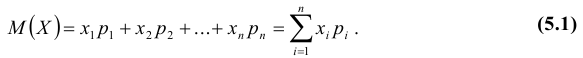
Свойства математического ожидания:

Мода

Модой Мо(Х) случайной величины Х называется ее наиболее вероятное значение (для которого вероятность pi или плотность вероятности f(x) достигает максимума).

Среднее квадратичное отклонение

Средним квадратическим отклонением (или стандартным отклонением) σ(Х) случайной величины Х называют значение квадратного корня из ее дисперсии:

Средним квадратическим отклонением (или стандартным отклонением) σ(Х) случайной величины Х называют значение квадратного корн
c1