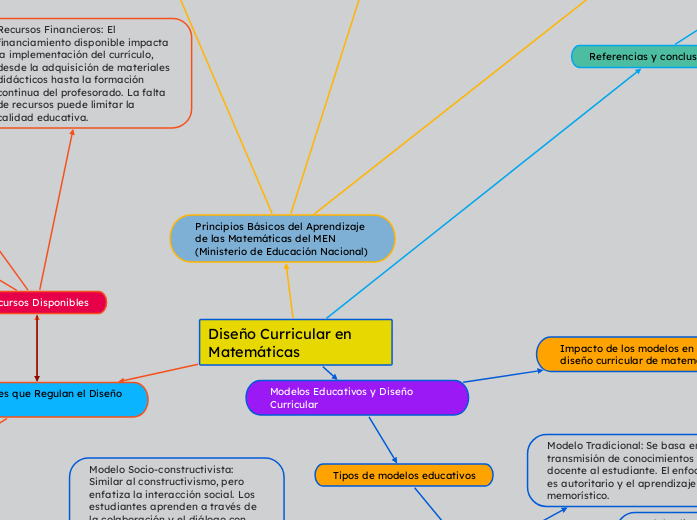
Diseño Curricular en Matemáticas
Modelos Educativos y Diseño Curricular
Tipos de modelos educativos
Los modelos educativos son enfoques sistemáticos que guían la enseñanza y el aprendizaje
Modelo Tradicional: Se basa en la transmisión de conocimientos del docente al estudiante. El enfoque es autoritario y el aprendizaje es memorístico.
Modelo Constructivista: Promueve la construcción activa del conocimiento por parte del estudiante. Se enfoca en la comprensión y la aplicación, fomentando la curiosidad y el pensamiento crítico.
Modelo Socio-constructivista: Similar al constructivismo, pero enfatiza la interacción social. Los estudiantes aprenden a través de la colaboración y el diálogo con sus pares.
Modelo Basado en Proyectos: Los estudiantes trabajan en proyectos a largo plazo que les permiten investigar y resolver problemas reales. Fomenta habilidades prácticas y el trabajo en equipo.
Modelo Flipped Classroom (Clase Invertida): Los estudiantes aprenden el contenido en casa (a través de videos o lecturas) y utilizan el tiempo de clase para actividades prácticas y discusiones.
Modelo Montessori: Fomenta la autonomía del estudiante y el aprendizaje a su propio ritmo, utilizando materiales didácticos diseñados específicamente para explorar conceptos.
Modelo por Competencias: Se centra en el desarrollo de habilidades y competencias específicas, integrando conocimientos teóricos y prácticos para la vida real.
Modelo Educativo Inclusivo: Busca atender a la diversidad del alumnado, adaptando metodologías y recursos para garantizar que todos los estudiantes tengan acceso a una educación de calidad.
Impacto de los modelos en el diseño curricular de matemáticas.
El impacto de los modelos educativos en el diseño curricular de matemáticas es significativo y puede manifestarse en varios aspectos
Enfoque de Aprendizaje
Promueve la comprensión profunda de conceptos matemáticos, donde los estudiantes construyen su conocimiento a través de la exploración y la resolución de problemas.
Estrategias Didácticas
Facilita la aplicación de conceptos matemáticos en proyectos reales, lo que aumenta la motivación y el interés de los estudiantes.
Evaluación
En modelos como el socio-constructivista, se da prioridad a la evaluación continua, donde se valora el proceso de aprendizaje más que solo los resultados finales.
Adaptación y Diversidad
Permite diseñar un currículo que contemple diversas estrategias y recursos para atender a estudiantes con diferentes necesidades y estilos de aprendizaje, asegurando que todos tengan oportunidades de éxito.
Uso de Recursos
En modelos modernos, el uso de software educativo, aplicaciones y herramientas digitales se integra al currículo, facilitando el aprendizaje interactivo y personalizado.
Interdisciplinariedad
Algunos modelos fomentan la conexión entre matemáticas y otras disciplinas, lo que permite a los estudiantes ver la relevancia de las matemáticas en diferentes contextos, como ciencias, arte y economía.
Condiciones que Regulan el Diseño Curricular
Políticas Educativas y Normativas
Lineamientos Gubernamentales: Las políticas educativas establecen los objetivos, principios y estándares que deben seguirse en el diseño curricular. Esto incluye normativas sobre contenidos, competencias y evaluaciones.
Currículo Nacional: Muchas veces, el currículo debe alinearse con un currículo nacional o regional, asegurando que se cumplan requisitos básicos de educación.
Inclusión y Diversidad: Las políticas también deben considerar la inclusión, garantizando que el currículo sea accesible para todos los estudiantes, independientemente de sus contextos y necesidades.
Necesidades Sociales y Comunitarias
Contexto Local: Las características culturales, económicas y sociales de la comunidad deben reflejarse en el currículo. Esto ayuda a que los estudiantes se identifiquen con su aprendizaje y lo consideren relevante.
Demanda del Mercado Laboral: Las habilidades y conocimientos que se enseñan deben alinearse con las necesidades del mercado laboral local, preparando a los estudiantes para un futuro profesional.
Participación Comunitaria: Involucrar a padres, estudiantes y miembros de la comunidad en el diseño curricular puede asegurar que se aborden sus expectativas y necesidades específicas.
Recursos Disponibles
Recursos Humanos: La calidad y formación del personal docente son cruciales. Un currículo bien diseñado necesita maestros capacitados que puedan implementarlo eficazmente.
Tecnología: La disponibilidad de herramientas tecnológicas puede enriquecer el currículo, permitiendo métodos de enseñanza más innovadores y accesibles.
Recursos Financieros: El financiamiento disponible impacta la implementación del currículo, desde la adquisición de materiales didácticos hasta la formación continua del profesorado. La falta de recursos puede limitar la calidad educativa.
Principios Básicos del Aprendizaje de las Matemáticas del MEN (Ministerio de Educación Nacional)
Desarrollo de Competencias Matemáticas Clave
Resolución de Problemas: Fomentar la habilidad de abordar y resolver problemas matemáticos en contextos reales. Esto incluye la identificación de situaciones problemáticas y la aplicación de estrategias adecuadas.
Razonamiento y Argumentación: Promover el pensamiento crítico y la capacidad de argumentar matemáticamente. Los estudiantes deben aprender a justificar sus respuestas y a analizar la validez de soluciones propuestas.
Comunicación Matemática: Desarrollar la capacidad de expresar ideas matemáticas de forma clara, tanto de manera oral como escrita, facilitando el diálogo y la discusión en clase.
Conexiones Matemáticas: Fomentar la relación de conceptos matemáticos entre sí y con otras áreas del conocimiento, ayudando a los estudiantes a ver la matemática como una herramienta útil en diversas disciplinas.
Enfoques Pedagógicos Recomendados
Aprendizaje Activo: Promover metodologías que involucren a los estudiantes en su propio proceso de aprendizaje, como el aprendizaje basado en proyectos, el trabajo en grupo y el uso de juegos matemáticos.
Enfoque Constructivista: Facilitar un entorno donde los estudiantes construyan su conocimiento a partir de experiencias previas, exploración y reflexión, en lugar de recibir información de forma pasiva.
Diferenciación: Adaptar las estrategias de enseñanza para atender la diversidad en el aula, reconociendo que los estudiantes tienen diferentes ritmos y estilos de aprendizaje.
Uso de Tecnología: Integrar herramientas tecnológicas que apoyen el aprendizaje, como software educativo, calculadoras y plataformas en línea que faciliten la práctica y la colaboración.
Evaluación del Aprendizaje en Matemáticas
Evaluación Formativa: Realizar evaluaciones continuas que permitan retroalimentar el aprendizaje y ajustar la enseñanza. Esto incluye observaciones, cuestionarios y autoevaluaciones.
Evaluación Sumativa: Aplicar evaluaciones al final de un período para medir el logro de los objetivos de aprendizaje, como exámenes y proyectos finales.
Diversidad de Instrumentos: Utilizar una variedad de métodos de evaluación (pruebas escritas, proyectos, presentaciones) para obtener una visión más completa del rendimiento del estudiante.
Reflexión sobre el Aprendizaje: Fomentar la autoevaluación y la reflexión por parte de los estudiantes sobre su propio proceso de aprendizaje, promoviendo la metacognición.
Referencias y conclusiones
Un diseño curricular en matemáticas bien estructurado no solo busca transmitir conocimientos, sino también desarrollar competencias críticas que preparen a los estudiantes para el futuro, promoviendo un aprendizaje significativo y relevante en un entorno inclusivo y dinámico.
Bibliografía
El diseño curricular debe ser flexible, permitiendo ajustes y mejoras basadas en la retroalimentación de docentes, estudiantes y la comunidad, así como en los cambios en las necesidades sociales y tecnológicas.