Estadística Descriptiva
Medidas
Dispersión
Máximo
Mínimo
Rango
Varianza
Coeficiente de variación
Desviación tipica
Centrales
Media
Mediana
Moda
Posición
Cuantiles
Percentiles
Representaciones gráficas
Gráfico de barras

Gráfico de sectores

Histogramas

Polígonos de frecuencia

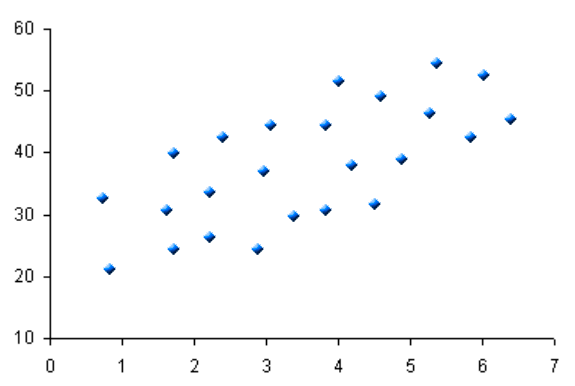
Diagrama de dispersión
Gráfica de caja y bigote

Es la rama de la estadística que se dedica a describir las características de un conjunto de datos
A través de
Cálculo de medidas de resumen
Clasificación y agrupamiento
Represenación gráfica
Tablas estadísticas
Variables
Cualitativas
Nivel de medición
Nominal
Ej: Estado civil de una persona: soltero, casado, divorciado,viudo.
Ordinal
Ej: Medallas de una competición: oro,plata, bronce.
Cuantitativas
Pueden ser
Continuas
Ej: La altura de 4 amigos: 1,73 , 1,80 , 1,78 , 1,84
Discreta
Ej: El numero de hermanos de 4 amigos: 2.1.3.1
Nivel de medición
Intervalo
Ej: La temperatura observada con un termómetro graduado en grados centígrados enteros: 15°C, 22!C
De razón
Ej: El peso de 4 amigos: 85,5 , 90 , 93,2 , 88,1
Población
Conjunto de datos formado por todas las medidas tomadas sobre un conjunto de elementos que tienen alguna característica en común
N= tamaño de la población
Unidad de análisis
Es la entidad principal que se está analizando en un estudio
Unidad de muestreo
Cada uno de los elementos que comprende la base de la muestra y que figuran numerados e individualizados en el registro
Parámetros
Función definida sobre los valores numéricos de características de una población
μ=promedio poblacional
σ 2= varianza poblacional
Tipos de población
Finita
Infinita
Blanco
Accesible
Muestra
Es un subconjunto de casos representativos de la población en estudio
Muestras probabilisticas
Todos los elementos de la población tienen la misma posibilidad de ser elegidos
Muestras no probabilisticas
Depende del proceso de toma de desiciones de una persona, tienden a ser sesgadas
Estadígrafos
Función definida sobre los valores observado de una muestra
x̄= media muestral
S2= varianza muestral
Elementos
Marco muestral
Listado de todas las unidades de muestreo disponibles que tienen probabilidad de formar parte de la muestra.
GuIa telefónica, padrón electoral
Tamaño muestral
Cantidad de unidades de estudio en la muestra y usualmente se simboliza con la letra n minúscula
n<30 muestra pequeña
n> 30 muestra grande
Alcance
# Descripción de características
# Resúmenes de casos
# Visualización e interpretación
# Identificación de tendencias
Dato
Es el registro de lo observado
Estructura tripartita
Unidad de Análisis
Variable
Valor, categoría o modalidad
Fuente de datos
Primaria
Los datos son producidos por el propio investigador
Secundaria
Los datos fueron producidos por otros investigadores
Directas
Indirectas
Variables bidimensionales
Tablas de contingencia
Es una tabla estadística que reúne en una
sola estructura toda la información
contenida en dos o más variables.
Usos mas frecuentes
Describir la composición de distintos subgrupos.
Comparar la composición de distintos subgrupos.
Observar la influencia de una variable sobre otra (VI -> VD).
Elaboración de conjeturas / formulación de hipótesis.
TABLAS p*k (p columnas * k filas)
Se construyen utilizando tablas de frecuencias
Frecuencias condicionales (en el interior de la tabla)
Frecuencias marginales de las filas
Frecuencias marginales de las columnas
Totales (de filas y columnas)
Es conveniente expresar en porcentajes las frecuencias marginales y totales
¿Cómo se interpreta su información?
TRATAMIENTO SIMÉTRICO
Se comparan los porcentajes obtenidos sobre el total del cuadro.
TRATAMIENTO ASIMÉTRICO
UNA VARIABLE ES “CAUSA” DE LA OTRA
Variable Independiente (VI) y Variable Dependiente(VD)
Se calculan los porcentajes en el sentido del factor causal (VI)
Se comparan los porcentajes obtenidos en el sentido contrario (VD)
Por convención
La variable Independiente se ubica en columnas
La variable Dependientese ubica en filas
Covarianza
Sxy
Sxy>0 indica relacion lineal directa
Sxy<0 indica relacion lineal inversa
Sxy=0
Puede indicar que
Las variables son independientes
Hay dependencia entre las variables, aunque la covarianza sea nula
Coeficiente de correlacion r de Pearson
r = Sxy /(Sx*Sy)
Dividimos la covarianza por el producto de las
desviaciones típicas de cada variable, obtenemos un
coeficiente adimensional
Propiedades
Carece de unidades de medida (Adimensional).
Es invariante para transformaciones lineales de las variables
Solo toma valores comprendidos entre -1 y 1.
Cuando lrl esté próximo a 1, se tiene que existe una relación lineal muy fuerte entre las variables.
Cuando r tiende a 0, puede afirmarse que no existe relación lineal entre las variables (variables incorreladas).