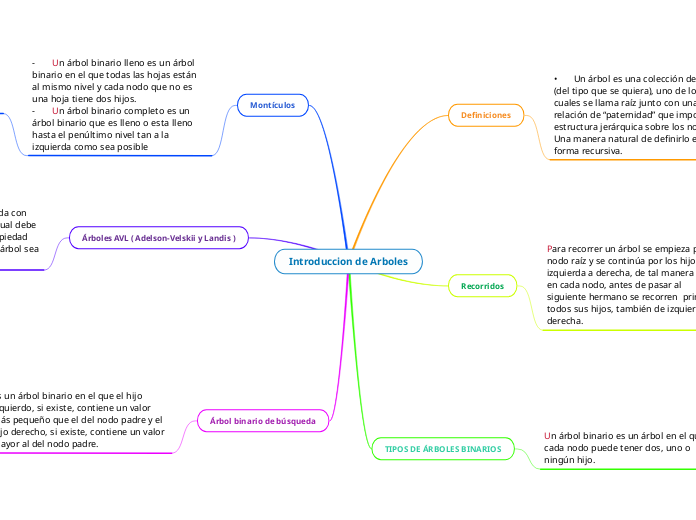
Introduccion de Arboles

• Un árbol es una colección de nodos (del tipo que se quiera), uno de los cuales se llama raíz junto con una relación de “paternidad” que impone una estructura jerárquica sobre los nodos.• Una manera natural de definirlo es de forma recursiva.

- Caso base: o el árbol esta vacío o tiene un solo nodo.
- Caso general: un nodo raíz ( r ) y cero o más subárboles A1, A2,..., An cada uno de ellos tiene su raíz conectada a r mediante una arista.

Para recorrer un árbol se empieza por el nodo raíz y se continúa por los hijos, de izquierda a derecha, de tal manera que en cada nodo, antes de pasar al siguiente hermano se recorren primero todos sus hijos, también de izquierda a derecha.

• Recorrido en orden previo o preorden: en este modo de recorrido, se trabaja en el nodo antes de pasar al siguiente.
• Recorrido en orden posterior o postorden: en este, se trabaja en cada nodo una vez que ya se ha trabajado con todos sus hijos y no antes.
• Recorrido en orden simétrico o inorden: en esta forma de recorrido se trabaja en los nodos hoja la primera y única vez que se pasa por ellos y en el resto de nodos la segunda vez.

Un árbol binario es un árbol en el que cada nodo puede tener dos, uno o ningún hijo.

- Un árbol binario lleno es un árbol binario en el que todas las hojas están al mismo nivel y cada nodo que no es una hoja tiene dos hijos.
- Un árbol binario completo es un árbol binario que es lleno o esta lleno hasta el penúltimo nivel tan a la izquierda como sea posible

Ejemplo

Valor máximo es 10 y se encuentra en la raíz del árbol.
Es un árbol binario completo ya que esta lleno hasta el penúltimo nivel y en el último nivel tiene los nodos a la izquierda.

Son árboles binarios de búsqueda con una condición de equilibrio, la cual debe ser fácil de mantener. Dicha propiedad asegura que la profundidad del árbol sea O (log n).

La idea de equilibrio más sencilla sería que los subárboles izquierdo y derecho fuesen igual de profundos, pero esto no evita que el árbol sea demasiado profundo.

Es un árbol binario en el que el hijo izquierdo, si existe, contiene un valor más pequeño que el del nodo padre y el hijo derecho, si existe, contiene un valor mayor al del nodo padre.

Aplicaciones de los árboles binarios de búsqueda y comparación con listas

- Facilita la búsqueda, aunque no facilita los accesos directos como sucedía con los arrays. Suministra un acceso más rápido y constante, así es conveniente para aplicaciones en las que el tiempo de búsqueda debe minimizarse.
- Ocupa más espacio que una lista enlazada (contiene un puntero extra).
- Los algoritmos para manipular el árbol son más complicados que los de las listas.