Las medidas estadísticas
Bivariantes de regresión
Regresión Lineal Simple
Cuando se relacionan una funcional entre la variable dependiente (y) e independiente (x) es una línea recta, se tiene una regresión lineal siempre.
Y = ßo + ß1X + ε
Las relaciones entre las variables pueden ser directas o también inversas.
relaciones
ßo : El valor de la ordenada donde la línea de regresión se intercepta al eje Y.
ß1 : El coeficiente de regresión poblacional (pendiente de la línea recta)
ε : El error.
según el autor F. de Mendiburu
Para elegir una relación funcional particular como la representativa de la población bajo
investigación, usualmente se procede:
1) Una consideración analítica del fenómeno que nos ocupa, y
2) Un examen de diagramas de dispersión.
Regresión Múltiple
Determinar la relación entre las variables independientes y dependiente, o variables de predicción y de criterio. La regresión múltiple permite añadir diversas variables, de modo que la ecuación refleje los valores de un cierto número de variables de predicción, no una sola. El objetivo de esto es mejorar las predicciones de la variable de criterio.
Rango
Explica el comportamiento de una variable y así predecir el valor de la variable de función de los valores dados de lo otro.
Su clasificación en función del numero de las variables explicativa de regresión y correlación y es simple si hay una variable explicativa es múltiple si el numero de variable explicativa son varias.
El análisis de regresión se trata de emplear métodos que permitan determinar la mejor relación funcional entre dos o mas variables
Y = f(x1,...,xn; θ1,...,θm)
Donde
Y : Variable respuesta (o dependiente)
xi : La i-ésima variable independiente (i=1,..,n)
θj : El j-ésimo parámetro en la función (j=1,..,m)
f : La función
Relación directa: la pendiente de esta línea es positiva, por que la variable
Y crece a medida que la variable X también lo hace.
relación directa
Relación inversa: La pendiente de esta línea es negativa, por que a medida
que aumenta el valor de la variable Y, el valor de la variable X disminuye
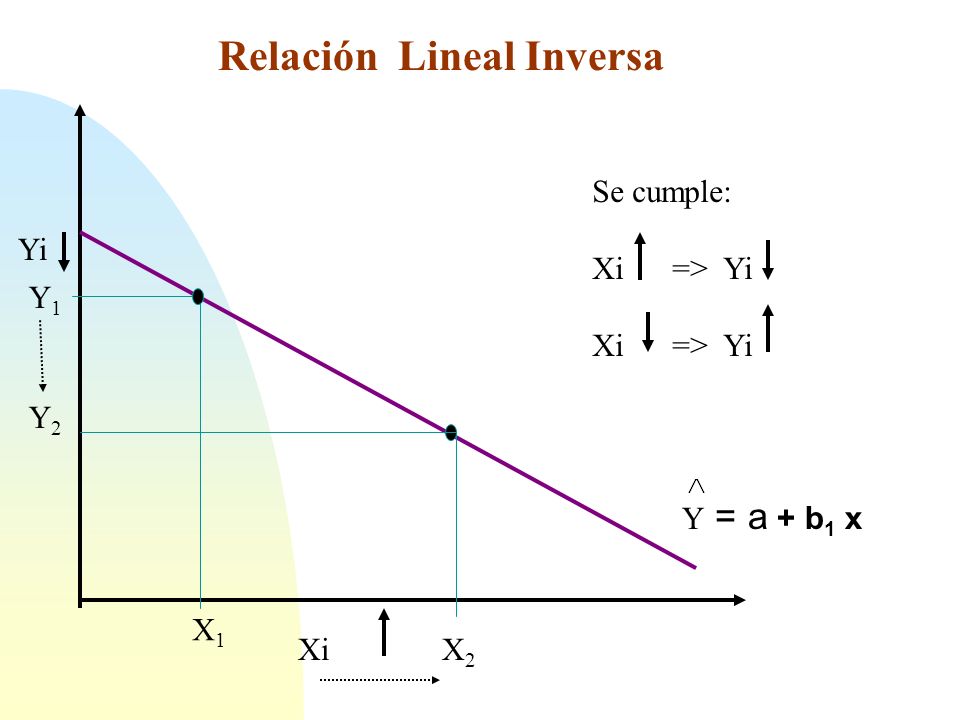
relación inversa
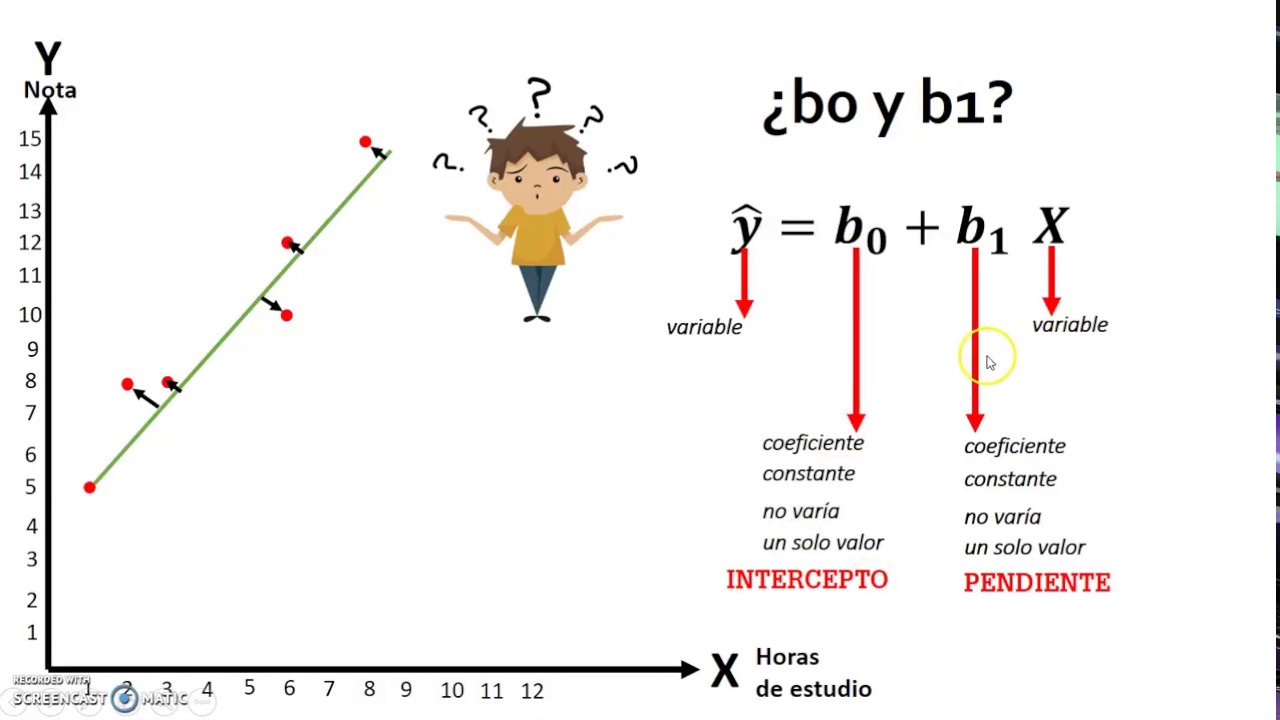
regresión lineal
Determina el grado de dependencia de la serie de los valores X y Y prediciendo el valor que se obtendrá para su valor X
Suposiciones de la regresión lineal
Según el autor F. de Mendiburu.
1. Los valores de la variable independiente X son "fijos".
2. La variable X se mide sin error (se desprecia el error de medición en X)
3. Existe una subpoblación de valores Y normalmente distribuido para cada valor de
X.
4. Las variancias de las subpoblaciones de Y son todas iguales.
5. Todas las medias de las subpoblaciones de Y están sobre la misma recta.
6. Los valores de Y están normalmente distribuidos y son estadísticamente
independientes.

1. determinar los parámetros ßo y ß1 a partir de los datos muestrales observados
2. De la ecuación (3), para un xi determinado, se tiene el correspondiente Yi , y el valor del error εi sería (Yi-ßo-ß1Xi)
3. Empleando el método de los mínimos cuadrados, es decir minimizando la suma de cuadrados de los errores, se determinan los valores de bo y b1,
Resolviendo las ecuaciones normales, se tiene

donde:
b0 : es el valor que representa (estimador) a ß0
b1 : es el valor que representa (estimador) a ß1
SPXY : denota a la suma de productos de X con Y,
SCX : denota a la suma de cuadrados de X.

Estimación de parámetros
El coeficiente de regressión (b1)
Está expresado en las mismas unidades de medida de la variable X. e indica el número de
unidades que varía Y cuando se produce cambio en una unidad en X (pendiente de la recta de
regresión).
Si b1=0, se dice que no existe relación lineal entre las dos variables y que estas son
independientes.
Fuentes de variación en la regresión lineal
Los cálculos de regresión pueden ser vistos como un proceso de partición de la suma total de
cuadrados
Se observa que la desviación total para un Yi en particular es igual a la suma de las desviaciones
explicada e inexplicada, simbolicamente.
(y y) (yˆ y) (y yˆ )

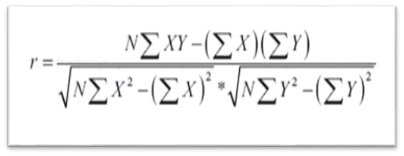
Correlación lineal simple.
El coeficiente de correlación (r) es un número que indica el grado o intensidad de asociación
entre las variables X e Y. Su valor varía entre -1 y +1
-1 ≤ r ≤ 1.
Según el autor F. de Mendiburu
Si r=-1, la asociación es perfecta pero inversa; es decir, a valores altos de una variable le
corresponde valores bajos a la otra variable, y viceversa.
Si r=+1, también la asociación es perfecta pero directa.
Si r=0, no existe asociación entre las dos variables.
Coeficiente de determinación
De la descomposición de la suma de cuadrados total, se obtuvo:
SCT = SCR + SCE
dividiendo ambos miembros por la SCT, se tiene:
1 = SCR/SCT + SCE/SCT
de este resultado, se define el COEFICIENTE DE DETERMINACION de la muestra, denotada
por r², como:
r² = 1 - SCE/SCT = SCR/SCT
r² = SC explicada/SC total
r² = error explicado/error total
Como SCR ≤ SCT, se deduce que 0 ≤ r² ≤1.
Nomenclatura modificada
Un marco de notación modificado y más formal es valioso para comentar el análisis de regresión múltiple. Considere el modelo de regresión general con tres variables de predicción.
Y = α + β1 X1 + β3X3 + ∊
Coeficiente de regresión parcial (o neta)
Según el autor Churchill, G.A. (2009).
Cantidad que resulta de un análisis de regresión múltiple e indica el cambio promedio en la variable de criterio por cambio unitario en una variable predictiva, en igualdad de circunstancias en todas los como variable de creación. La interpretación se aplica sólo cuando las variables de predicción son independientes entre sí, como se requiere para la aplicación válida del modelo de regresión múltiple. (pág 688)

En esta ecuación más precisa, tiene validez lo siguiente:
Y(123) es e‘ valor de Y que se calcula a partir de la ecuación de regresión, con Y como variable de criterio y X1, X2 y X3 como variables de predicción
α(123) es el parámetro de intersección en la ecuación de regresión múltiple, con F como variable de criterio Y X1 X2 y X3 como variables de predicción
s de predicción (k = 3) y dos subíndices secundarios
β(123) es el coeficiente de X1 en la ecuación de regresión, con Y como variable de criterio y X, X2 y X3 como variables de predicción o explicativas. Se le llama coeficiente de regresión parcial (o neta).
Su número varía desde cero en la regresión simple hasta cualquier número k – 1, donde se tienen k variables de predicción en el problema. En este caso, el modelo contiene tres variable
ε(123) es el error relacionado con la predicción de Y cuando Xi X2 y X3 son las variables de predicción.

Supuesto de multicolinealidad
Los supuestos relativos al término de error en el modelo de regresión simple se aplican también a la ecuación de regresión múltiple. Es la relación lineal perfecta o exacta entre algunas o todas las variables explicativas.

Coeficientes de regresión parcial
Indicativa de que la variable de criterio, las ventas en un territorio, se predecirá con dos variables de predicción, X1 y X2.
• Para el modelo de regresión con 3 variables se puede calcular 3 coeficientes correlación.
• Mide el grado de asociación lineal entre 2 variables
• R12.3: coeficiente de correlación parcial entre Y y X, mantiene X3 constante
• R13.2: coeficiente de correlación parcial entre Y y X3, mantiene X2 constante
• R23.1:coeficiente de correlación parcial entren X2 y X3, manteniendo y constante.

Subtopic
Coeficientes de correlación múltiple y de determinación múltiple
Es de gran criterio de regresión simple, es la medida de la magnitud de la relación entre variables de criterio y predicción.
Coeficiente de determinación múltiple
En el análisis de determinación múltiple, la proporción de variación en la variable de criterio que se explica con la covariación de las variables predictivas.
Coeficiente de correlación múltiple
En el análisis de regresión múltiple, la raíz cuadrada del coeficiente de determinación múltiple.
• Ry123, donde el subíndice primario es la variable de criterio, y los subíndices secundarios, las variables de predicción.
• Por su parte, el coeficiente de determinación múltiple se denota formalmente con Ry.1232 e informalmente con R2 y es la proporción de la variación de la variable de criterio que se compone de la covariación en las variables de predicción.
• Cuando se investiga la relación de las ventas con los anuncios televisivos y el número de representantes de ventas, Ry.122 = 0.874.
• La raíz cuadrada de dicha cantidad, Ry.12 = 0.935, es el coeficiente de correlación múltiple, que siempre se expresa como número positivo.

Coeficientes de correlación parcial
• Dos cantidades adicionales, se interpretan los resultados de análisis de regresión múltiple y no se incluyen en el de regresión simple.
• El coeficiente de correlación parcial y valor elevado al cuadrado, el coeficiente de determinación parcial.
Coeficiente de determinación parcial
Cantidad que resulta del análisis de regresión múltiple e indica la proporción de variación de la variable de criterio que no se explica con una o más variables previas y sí con la inclusión de una nueva variable a la ecuación de regresión.
Coeficiente de correlación parcial
En el análisis de regresión múltiple, la raíz cuadrada del coeficiente de determinación parcial.
>Se definió el coeficiente de determinación parcial para el número de representantes de ventas (X2) como rY2.12
>Se denotará como rY1.22 y sería el porcentaje de la variación de las ventas no relacionado con X2 que guarda relación creciente con este último coeficiente mostraría la contribución incremental de X1 después de considerar la relación de Y con X2.
Variables binarias
Y = α + β1X1 + β2 X2 + β3X3+ ε
Xi = 0, si se trata de una mujer
Xi= 1, si se trata de un hombre
Una a la que se asigna uno de dos valores, 0 o 1, y se usa para representar en forma numérica los atributos o características que no son esencialmente cuantitativos.
• Esta técnica se amplía fácilmente para el manejo de clasificaciones de dos o más categorías.
• Es de máxima importancia que el analista preste atención a la codificación de las variables cuando interpreta los resultados de una regresión en que se utilizan variables binarias
• Con m categorías puede representarse de manera no ambigua con un conjunto de m – 1 variables binarias, en que el w-ésimo binario sería superfluo.
• Suponga que se utilizan tres variables binarias para representar las cuatro categorías del índice de eficiencia de distribuidores.
El modelo de regresión es:
Y α + β1X1 + β2X2 + β3X3 + β4X4 + β5X5 ε

Trasformaciones de variables
Hace posible añadir variables con escalas de clasificación y nominales a los problemas de regresión.
Dícese del cambio en la escala con que se expresa una variable.
A primera vista, parecería imposible estimar los parámetros α, β1, β2 y β3 con los procedimientos normales de cuadrados mínimos
1) se toman los logaritmos naturales de Y y de cada una de las X;
2) se despejan las ecuaciones resultantes con los procedimientos normales de cuadrados mínimos;
3) se toma el antilogaritmo de α‘ para derivar una estimación de a, y
4) se leen los valores de βi; ya que son los mismos en ambos modelos.
La relación entre la variable de criterio y las variables de predicción es aditiva
La relación entre las variables de criterio y de predicción es lineal
Los errores son homoscedásticos (es decir, son iguales a una constante sin importar el valor de las variables de prediccióne