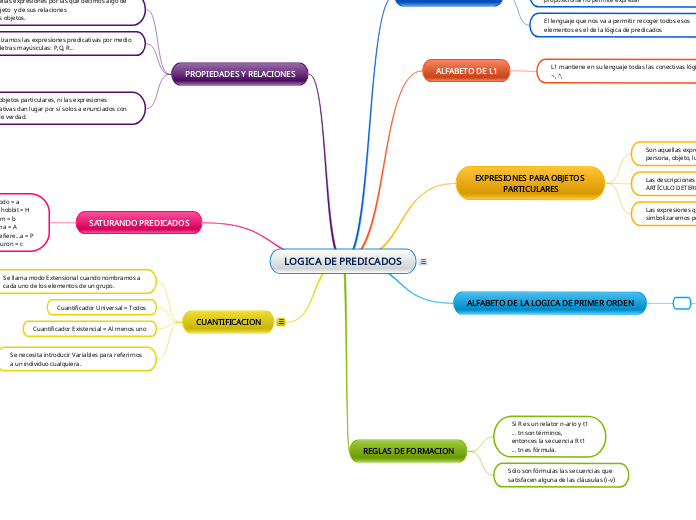
LOGICA DE PREDICADOS
LENGUAJE EXPRESIVO
No permite identificar elementos que se repiten dentro de las oraciones
Hay muchos argumentos válidos que el lenguaje de la lógica proposicional no permite expresar
El lenguaje que nos va a permitir recoger todos esos elementos es el de la lógica de predicados
ALFABETO DE L1
L1 mantiene en su lenguaje todas las conectivas lógicas de L0: ¬, ^,
EXPRESIONES PARA OBJETOS
PARTICULARES
Son aquellas expresiones que identifican un individuo, sea persona, objeto, lugar
Las descripciones definidas son construcciones del tipo:
ARTÍCULO DETERMINADO + SINTAGMA NOMINAL
El portador del anillo
El mejor amigo del portador del anillo
Las expresiones que nombran objetos particulares las
simbolizaremos por las letras minúsculas.
Cada letra identifica a un individuo
ALFABETO DE LA LOGICA DE PRIMER ORDEN
-Constantes individuales: a, b, c, a1
-Variables individuales: x, y, z, x1
-Predicados o relatores: P, Q, R, R1
-Identidad: =, ≠
-Auxiliares: ), (, ], [
REGLAS DE FORMACION
Si R es un relator n-ario y t1
... tn son términos,
entonces la secuencia R t1
... tn es fórmula.
Sólo son fórmulas las secuencias que
satisfacen alguna de las cláusulas (i-v)
PROPIEDADES Y RELACIONES
Son aquellas expresiones por las que decimos algo de
algún objeto y de sus relaciones
con otros objetos.
Simbolizamos las expresiones predicativas por medio
de las letras mayúsculas: P,Q, R...
Ni los objetos particulares, ni las expresiones
predicativas dan lugar por sí solos a enunciados con
valor de verdad.
Obtenemos éstos cuando combinamos
ambos tipos de expresiones
MONARIOS a los predicados con un solo argumento
BINARIOS a los que tienen 2
TERNARIOS a los que tienen 3
SATURANDO PREDICADOS
Frodo = a
Es hobbit = H
Sam = b
Ama = A
Prefiere...a = P
Sauron = c
Frodo es Hobbit = Ha
Frodo ama a Sam = Aab
Sauron prefiere a Frodo antes que a Sam = Pcab
CUANTIFICACION
Se llama modo Extensional cuando nombramos a
cada uno de los elementos de un grupo.
No sirve para conjuntos infinitos
Cuantificador Universal = Todos
Cuantificador Existencial = Al menos uno
Se necesita introducir Variables para referirnos
a un individuo cualquiera.
Cuando en una fórmula sustituimos una
variable x por un individuo a, estamos diciendo que a
cumple las condiciones establecidas por la fórmula