Parábolas
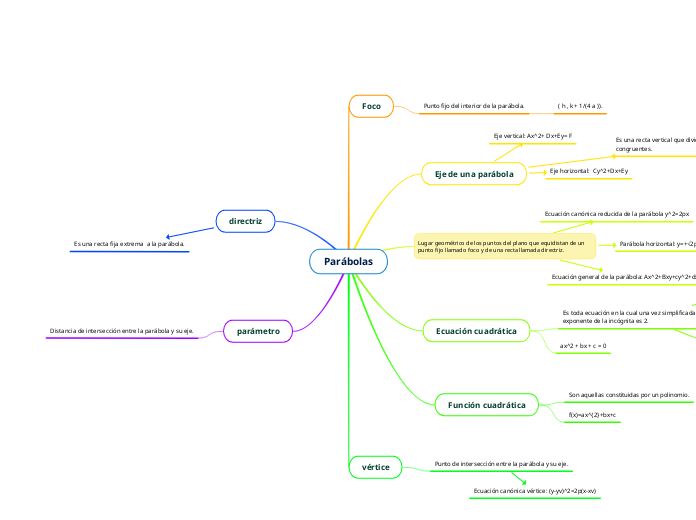
Foco
Punto fijo del interior de la parábola.
( h , k + 1/(4 a )).
Eje de una parábola
Es una recta vertical que divide la parábola en dos mitades congruentes.
Eje vertical: Ax^2+ Dx+Ey= F
Eje horizontal: Cy^2+Dx+Ey
Lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado foco y de una recta llamada directriz.
Ecuación canónica reducida de la parábola y^2=2px
Parábola horizontal: y=+√2px, Y=-√2px
Ecuación general de la parábola: Ax^2+Bxy+cy^2+dx+ey=f
Ecuación cuadrática
Es toda ecuación en la cual una vez simplificada el mayor exponente de la incógnita es 2.
Ecuaciones cuadráticas completas
Son ecuaciones de la forma ax2 + bx + c = 0 que tienen un término x2, un término x y un término independiente de x.
Ecuaciones cuadráticas incompletas
Son ecuaciones de la forma ax2 + c = 0 que carecen del término x o de la forma ax2 + bx = 0 que carecen del término independiente.
Resolución de ecuaciones cuadráticas
Es hallar las raíces de la ecuación. Para ello hacemos uso de la fórmula: x = [ – b ± √(b2 – 4ac) ] / 2a
ax^2 + bx + c = 0
Función cuadrática
Son aquellas constituidas por un polinomio.
f(x)=ax^{2}+bx+c
vértice
Punto de intersección entre la parábola y su eje.
Ecuación canónica vértice: (y-yv)^2=2p(x-xv)
directriz
Es una recta fija extrema a la parábola.
parámetro
Distancia de intersección entre la parábola y su eje.