Example:
Example:
Example:
This component accounts for anything else unexplained or irregular.
Explains the systematic and calendar- related movements of time series.
Describes behavior in long-term without accounting for seasonal or cyclical effects.
Danger
Extrapolation
Interpolation
Ice cream sales =
Suppose that the temperature = 35 degrees C
type of prediction for time series.

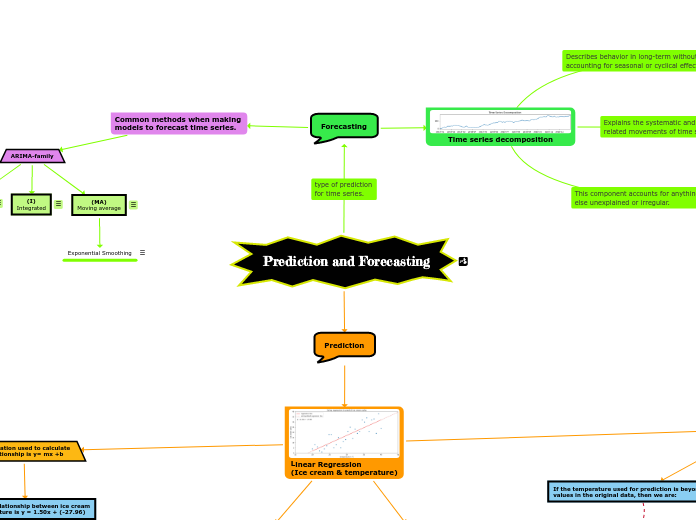
Prediction and Forecasting

m

Prediction

Linear Regression (Ice cream & temperature)

Linear Regression
(Ice cream & temperature)

Dependent variable

The quantity we want to predict
(Ice cream sales)

Independent variable

The variable we will use to predict it
(Temperature)

The equation used to calculate
the relationship is y= mx +b

The linear relationship between ice cream
and temperature is y = 1.50x + (-27.96)

ice cream sales = 1.50 x (temperature = x) -27.96

ice cream sales = 1.50 x (35) - 27.96

24.54 ice creams

Predictions

Temperature value used for prediction is within the range of original data points used to build regression

Making predictions from the solid portion of the line

If the temperature used for prediction is beyond the values in the original data, then we are:

Making predictions from the dotted portion of the line.

Trends don't continue indefinitely. If it is too hot people might not leave their A.C. cooled home, resulting in no sales.

Forecasting

Time series decomposition

Time series decomposition

Trend component

Trend component

The population of Earth is increasing,
or the value of a stock is stagnating.

seasonality component

seasonality component

The number of ice cream trucks
is higher in the summer months.

cyclical component

cyclical component

Hurricane driving the number of ice cream trucks down in the short-term because it isn't safe to be outside.

Common methods when making
models to forecast time series.

ARIMA-family

(AR)
autoregressive

r

Autoregressive models take advantage of the fact that an observation at time $t$ is correlated to a previous observation, for example at time t-1.Note that not all time series are autoregressive.

(I)
Integrated

r

The integrated component concerns the differenced data or the change in the data from one time to another.

(MA)
Moving average

r

The moving average component uses a sliding window to average the last x observations where x is the length of the sliding window.

Exponential Smoothing

r

The moving average puts equal weight on each time period in the past involved in the calculation. In practice, this isn't always a realistic expectation of our data. Sometimes all past values are important, but they vary in their influence on future data points. For these cases, we can use exponential smoothing, which allows us to put more weight on more recent values and less weight on values further away from what we are predicting.