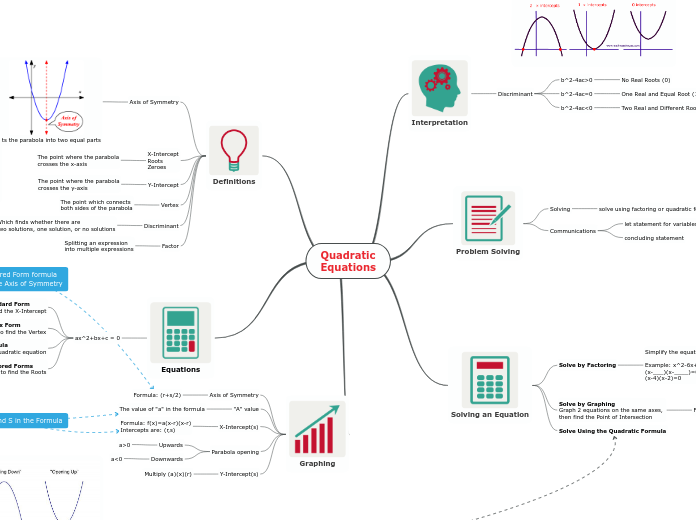
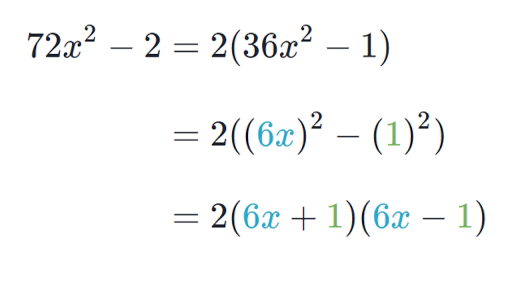Quadratic
Equations

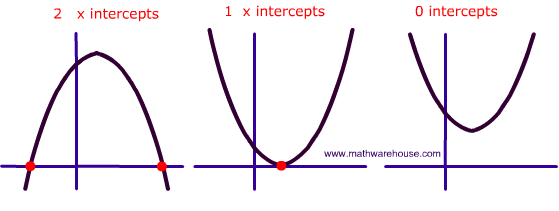
Discriminant

b^2-4ac>0

No Real Roots (0)

b^2-4ac=0

One Real and Equal Root (1)

b^2-4ac<0

Two Real and Different Roots (3)

Solving

solve using factoring or quadratic formula

Communications

let statement for variables

concluding statement

Solve by Factoring

Simplify the equation

Example: x^2-6x+8=0
(x-___)(x-____)=0
(x-4)(x-2)=0

Zero Product Property
When equation has product of two simple
equations, one of the two (or both) must be equal to zero

Example: (x-4)(x-2)

(x-4)=0 because x=4 and/or
(x-2)=0 because x=2

1) Factor
2) Find the 2 Solutions
3) Solve each Equation

Solve by Graphing
Graph 2 equations on the same axes,
then find the Point of Intersection

Finding the Point of Intersection

1) solve for x
2) plug the value of x into the
original equation to find y

Solve Using the Quadratic Formula

Axis of Symmetry

X-Intercept
Roots
Zeroes

The point where the parabola
crosses the x-axis

Y-Intercept

The point where the parabola
crosses the y-axis

Vertex

The point which connects
both sides of the parabola

Discriminant

Which finds whether there are
two solutions, one solution, or no solutions

Factor

Splitting an expression
into multiple expressions

ax^2+bx+c = 0

Standard Form
To find the X-Intercept

y=ax^2+bx+c

Vertex Form
Used to find the Vertex

Vertex
y = a(x – h)^2 + k

Quadratic Formula
Used to solve a quadratic equation

(-b±√b^2-4ac) / 2a

Factored Forms
Used to find the Roots

f(x) = a(x-r )(x-r )

Axis of Symmetry

Formula: (r+s/2)

"A" value

The value of "a" in the formula

X-Intercept(s)

Formula: f(x)=a(x-r)(x-r)
Intercepts are: (r,s)

Parabola opening

Upwards

a>0

Downwards

a<0

Y-Intercept(s)

Multiply (a)(x)(r)