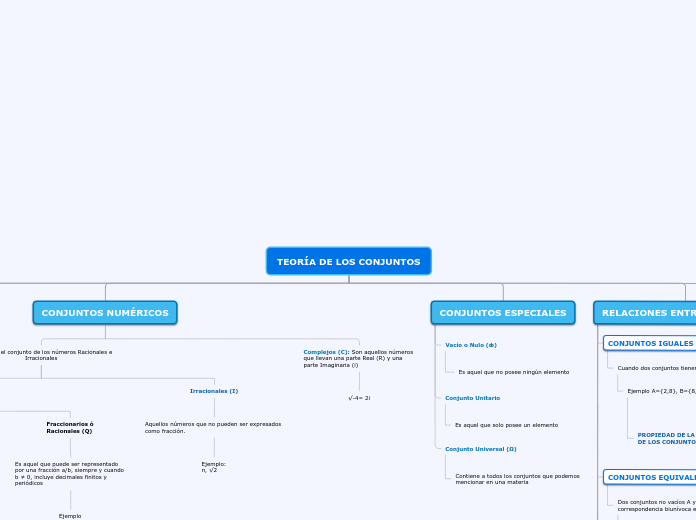
TEORÍA DE LOS CONJUNTOS

Agrupación o colección de cualquier tipo de
objetos que tienen propiedades comunes

Está compuesta por elementos y se
denotan con letras Mayúsculas

Ejemplo: A={1,2,3,4} “A" es el conjunto
de cuyos elementos son 1,2,3,4

Finito

Cuando el conjunto tiene un primer
y último elemento

Ejemplo: A={2,4,6,8}

Infinito

Cuando los elementos no tienen fin o
último elemento

Ejemplo B={2,4,6,….8n,…}

Por extensión

Cuando se conocen individualmente todos
sus elementos.

Ejemplo: B={a,e,i,o,u}

Por comprensión

Cuando éste se define por medio de una propiedad,
la cual debe satisfacer a cada uno de sus elementos

a. B={x / x, es una vocal}

Reales: Es el conjunto de los números Racionales e Irracionales

Racionales

Enteros (Z)

Está constituido por los enteros
positivos, negativos, incluyendo
al cero

Ejemplo:
-6, 10

Naturales (N)

Sus elementos son empleados
para realizar las operaciones de
contar. “Números Positivos”

Ejemplo:
1, 6

Fraccionarios ó
Racionales (Q)

Es aquel que puede ser representado
por una fracción a/b, siempre y cuando
b ≠ 0, incluye decimales finitos y
periódicos

Ejemplo
1/3, 4/2

Irracionales (I)

Aquellos números que no pueden ser expresados
como fracción.

Ejemplo:
π, √2

Complejos (C): Son aquellos números
que llevan una parte Real (R) y una
parte Imaginaria (i)

√-4= 2i

Vacío o Nulo (Φ)

Es aquel que no posee ningún elemento

Conjunto Unitario

Es aquel que solo posee un elemento

Conjunto Universal (Ω)

Contiene a todos los conjuntos que podemos
mencionar en una materia

Cuando dos conjuntos tienen los mismos elementos

Ejemplo A={2,8}, B={8,2}

PROPIEDAD DE LA IGUALDAD
DE LOS CONJUNTOS

Reflexiva: Un conjunto, siempre será igual a sí mismo

Ejemplo: A=A

Simétrica: Si un conjunto A es igual al conjunto B, entonces B será igual a A

Ejemplo A=B, → B=A

Transitiva: Si un conjunto A, es igual a B y B es igual a C, entonces A=C

Ejemplo: A=B y B=C → A=C

Dos conjuntos no vacíos A y B, son equivalentes, si existe una correspondencia biunívoca entre todos sus elementos

Ejemplo: A{1,2,3}, B{a,b,c}
1→a, 2→b, 3→c
Por lo tanto A≡B

Un conjunto A, está incluido en un conjunto B, si todo elemento de A es también elemento de B

Ejemplo:
A={1, 2, 3} y B={1, 2, 3, 4},

Entonces: A ⊂ B

Ejemplo:
A={0, 1, 2, 3} y B={1, 2, 3},

Entonces: A ⊄ B

PROPIEDAD DE
LOS SUBCONJUNTOS

Reflexiva: Si un conjunto, está incluído en sí mismo

Ejemplo: A ⊂ A

Antisimétrica: Si el conjunto A está incluído en conjunto B,
y B en A, el conjunto A es igual a B

Ejemplo A ⊂ B y B ⊂ A → A=B

Transitiva: Si un conjunto A, está incluido en un conjunto B y B está incluido en conjunto C, entonces A estará incluido en C

Ejemplo: A ⊂ B y B ⊂ C → A ⊂ C

Cuarta Propiedad: Para todo conjunto A, se cumple que el conjunto vacío, está incluido en el conjunto A

Dos conjuntos A y B, son disjuntos, si no tienen ningún elemento en común

Ejemplo:
A={1, 2, 3} y B={a, b, c}, entonces A y B son disjuntos

Dos conjuntos A y B, son comparables si uno
de los conjuntos es subconjunto del otro

Ejemplo:
A={2, 4, 6} y B={1, 2, 3, 4, 5, 6,},
entonces A ⊂ B son comparables

Ejemplo:
A={2, 3, 4} y B={4, 5, 6,},
entonces A ⊄ B no son comparables

Es el conjunto que tiene como elementos a
otros conjuntos

P{{1,2},{a,b},0}

Cuando el conjunto A, es el conjunto formado
por todos los subconjuntos de conjunto de A

Ejemplo:
A={a,b,c}
P(A)={{a,b,c,},{a,b},{a,c},{b,c},0}

Son todos los subconjuntos de A, que no sean
iguales al conjunto A

Ejemplo:
A={a,b,c}
P(A)={{a,b},{a,c},{b,c},0}