Vectors CPT
Jagbir Bhullar
MCV4U1-03

Distance Between 2 points
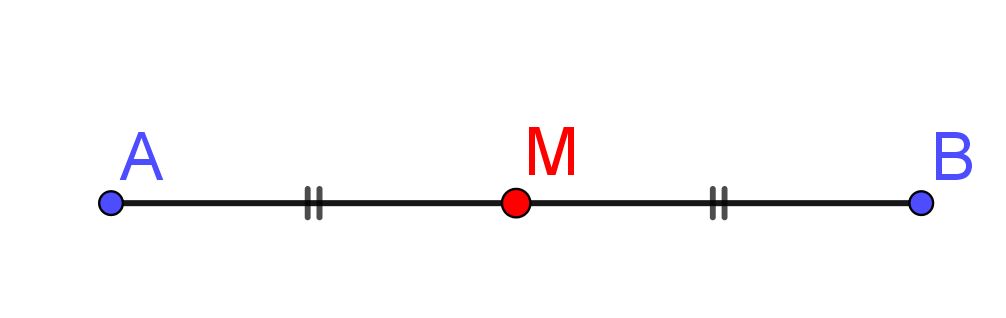
Midway between points

Collinear points
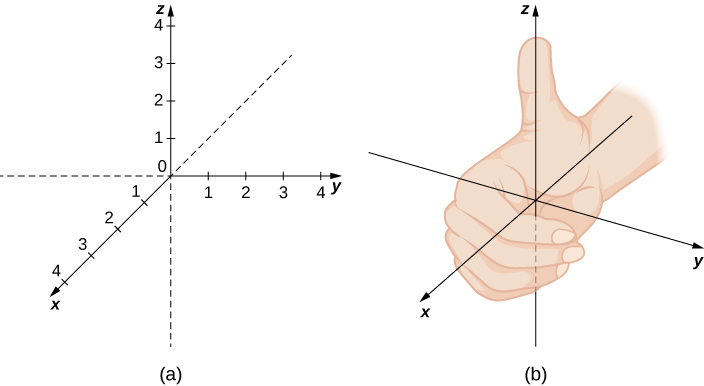
Vector Introduction
Points

Equal Vectors
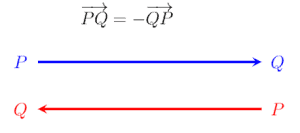
Zero Vector
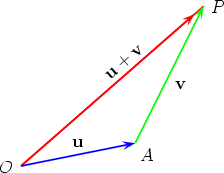
Triangle law of addition

The Vector
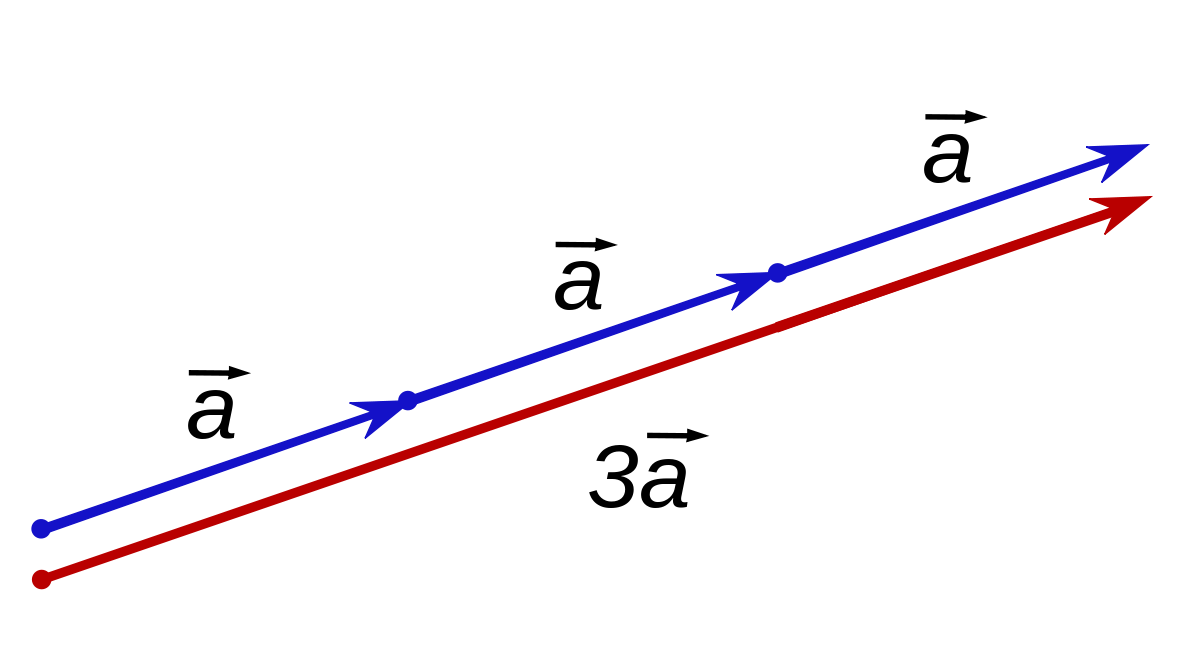
Scalar Multiplication
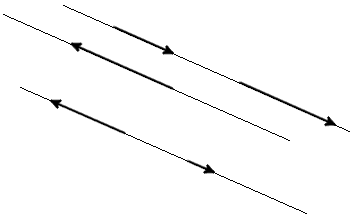
Collinear Vectors

Properties of Vector addition

Commutative property of addition
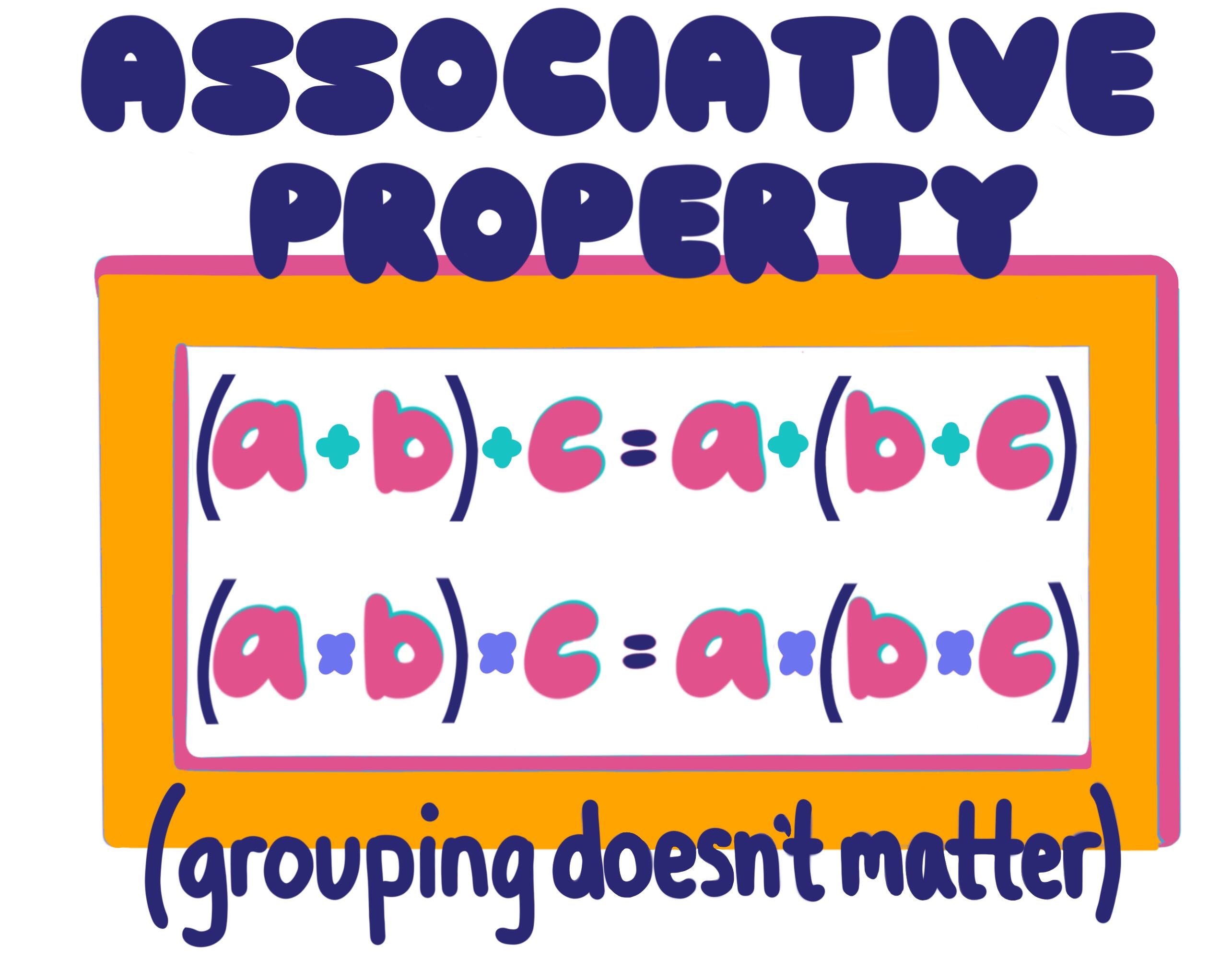
Associative Property of Addition
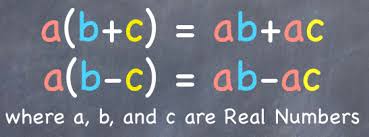
Distributive Property of Addition
Real Life Application

Architecture
Sports
Medical Tools

Dot Product

Cross Product
Intersection of 3 Planes
Lines and Planes

Rearranged

Commutative

Distributive

Magnitudes

Associative
Projections

Scalar Projections

Vector Projections

Calculations

Find a,b,c

Distributive Law

Scalar Law

not commutative

Skew Lines
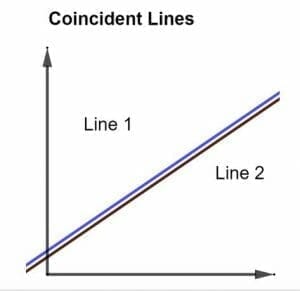
Coincident Lines

Parallel Lines

Equation of Lines in R2
Slope and Direction Vectors
Equations in R3

Parametric

Symmetric

Plane

Line

cartesian equation

parametrics

Parametric
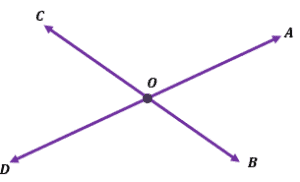
intersecting lines at a point

Intersecting

Coincident

Parallel

Skew
2 Planes

Coincident

Parallel

Intersect at line

Point to Line with cartesian coordinate

Point to Line with vector equation

Point to Plane

Intersects π at a point

Line Parallel to π

Line is on π

2 planes intersecting at line

2 parallel planes

2 coincident planes

3 planes intersect at 1 point

3 planes are parallel

2 planes are parallel 2 planes are
parallel and distinct the third is
not parallel

3 coplanar but not parallel
Line and plane
2 planes
3 planes

3 planes are coincident