Oscilación Hărți Mentale - Galeria publică
Explorați vasta noastră colecție publică de oscilación hărți mentale create de utilizatorii Mindomo din întreaga lume. Aici, puteți găsi toate diagramele publice legate de oscilación. Puteți vizualiza aceste exemple pentru a obține puțină inspirație. Unele diagrame vă oferă, de asemenea, dreptul de a le copia și edita. Această flexibilitate vă permite să folosiți aceste hărți mentale ca șabloane, economisind timp și oferindu-vă un punct de plecare solid pentru munca dvs. Puteți contribui la această galerie cu propriile diagrame, odată ce le faceți publice, și puteți fi o sursă de inspirație pentru alți utilizatori și să fiți inclus aici.
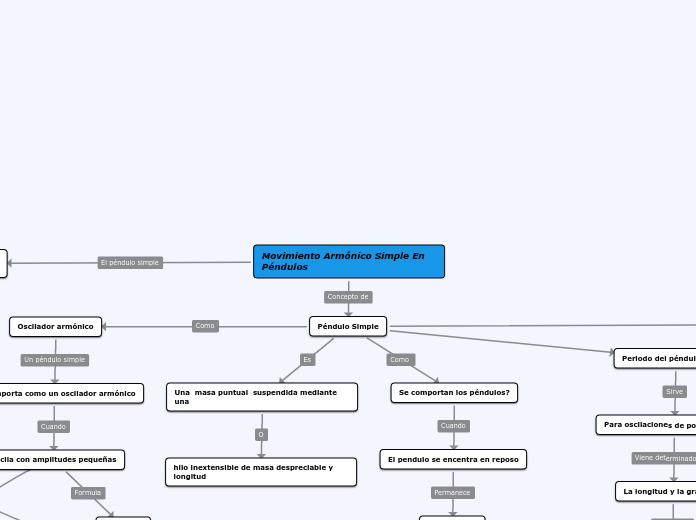

Movimiento Armónico Simple En Péndulos
după Cristian Mira

movimiento oscilatorio
după KAREN BUITRAGO

Movimiento Armónico Simple.
după Alejandro Soto

Movimiento Periodico
după Karla Ayala Morales

Movimiento Armónico Simple
după 'Andres Sossa'
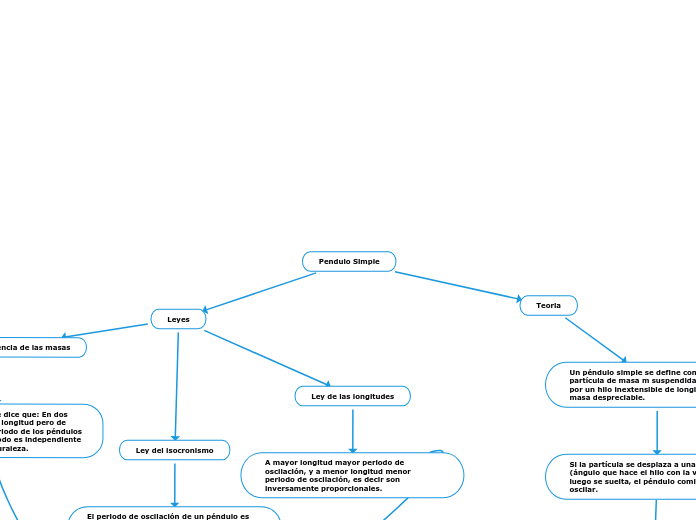

Pendulo Simple
după MURO DIAZ MURO DIAZ
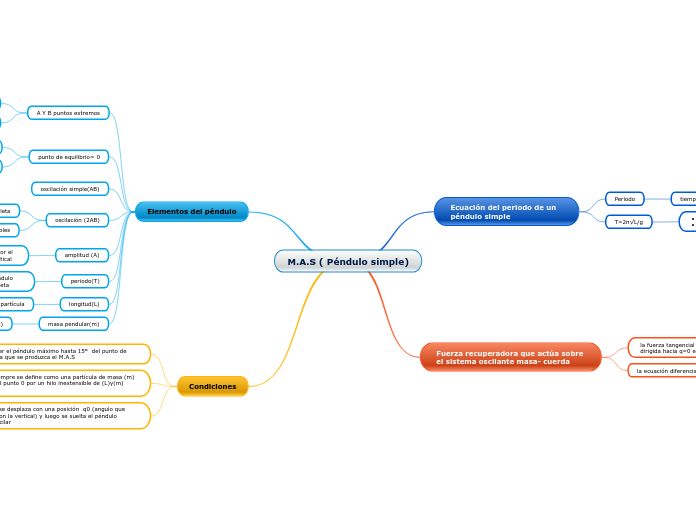

M.A.S ( Péndulo simple)
după Jefferson Sosa

LAS ONDAS
după julissa anabel chavarria boniche

¿Qué es una onda electromagnética?
după joulemar joulemar

Mapa E
după Juan Pis Gutiérrez

Pendulo Simple
după Carlos Alberto Lopez Badillo

Método científico (oscilación de la vela) (1)
după Alessandra Andrea Natsumi Guevara Rojas
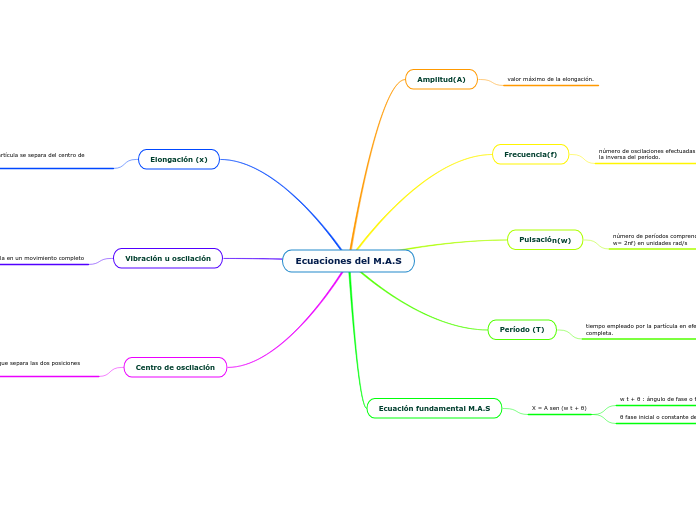

Ecuaciones del M.A.S
după ANA MARIA PUENTE MERA
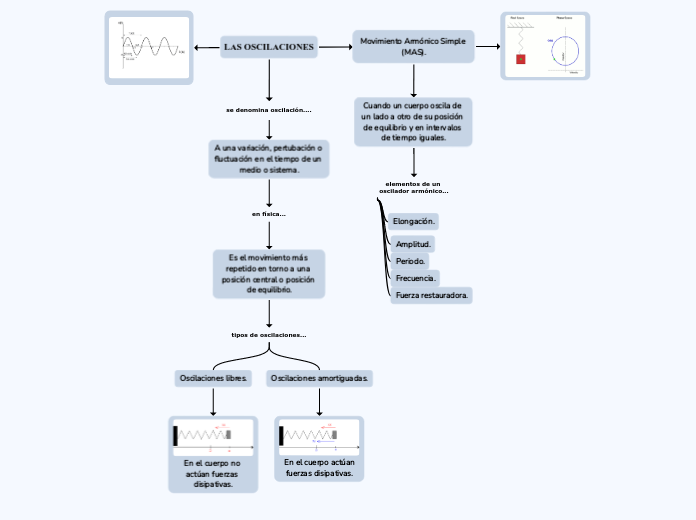

LAS OSCILACIONES
după souylusw souylusw

Marcha y sus componentes
după Ana Rojas Ramos
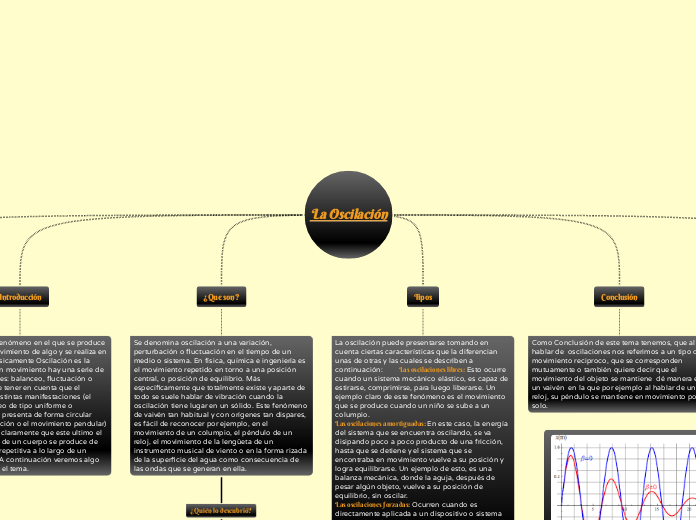

La Oscilación Fisica
după PRISCILA JAMILETH PALACIOS ALULIMA

Oscilacion
după SHAYLA NAYLED MENDOZA PARRAGA

FUNCIONES NO LINEALES APLICACIÓN EXPERIMENTAL PÉNDULO SIMPLE
după Juan Pablo Arias Aguirre

Oscilación (1) (1)
după Javier Andres Alava Chica

Oscilacion
după Caroline Doislé Yánez Moreira


OSCILACIONES Se denomina oscilación a una variación, perturbación o fluctuación en el tiempo de un medio o sistema. En física, química e ingeniería es el movimiento repetido en torno a una posición central, o posición de equilibrio. ¿Qué es una oscilación? Oscilación es la expresión de algo en movimiento En este último caso, el cambio de posición de un cuerpo se produce de manera periódica y repetitiva a lo largo de un periodo de tiempo. El ejemplo más conocido de movimiento oscilatorio o pendular es el que se produce en los péndulos en algunos relojes, Efectuar movimientos de vaivén a la manera de un péndulo o de un cuerpo colgado de un resorte o movido por él ¿Cuáles son los sistemas oscilantes? Un sistema oscilará alrededor de la posición de equilibrio si a un desplazamiento x, desde el equilibrio tiene como respuesta una fuerza que tiende a restaurar el sistema hacia la posición x=0. El tipo más simple ocurre cuando la fuerza restauradora está linealmente relacionada con el desplazamiento x. Como se representa En física, el período de una oscilación u onda (T) es el tiempo transcurrido entre dos puntos equivalentes de la onda. El concepto aparece tanto en matemáticas como en física y otras áreas de conocimiento. ¿Cuáles son los tipos de oscilaciones? -Oscilaciones libres. -Otros osciladores. -Oscilaciones amortiguadas. -Oscilaciones forzadas. -Osciladores acoplados. -Régimen caótico. Oscilaciones libres Si un cuerpo en oscilación es desplazado de su posición de reposo y ninguna fuerza es aplicada sobre el mismo posteriormente, se dice que está oscilando libremente. Otros osciladores un circuito que produce una oscilación propia de frecuencia, for- ma de onda y amplitud determinadas. Se estudiarán los osciladores senoidales. Según habíamos visto, un sistema realimentado puede ser oscilante a causa de una inestabilidad. Oscilaciones Amortiguadas se disipa energía mecánica debido a algún tipo de rozamiento. Cuando consideramos esta disminución de energía llamamos al oscilador 'amortiguado'. Oscilaciones forzadas La amplitud de una oscilación amortiguada decrece con el tiempo. Al cabo de un cierto tiempo teóricamente infinito, el oscilador se detiene en el origen. Para mantener la oscilación es necesario aplicar una fuerza oscilante. Oscilaciones acoplados La amplitud de una oscilación amortiguada decrece con el tiempo y con un cierto tiempo teóricamente infinito, el oscilador se detiene en el origen, para mantener la oscilación es necesario aplicar una fuerza oscilante. Régimen caótico Un sistema que experimenta un movimiento caótico nunca se repite a sí mismo, sino que más bien se comporta de forma continuamente diferente, el movimiento puede parecer totalmente aleatorio y desordenado, el movimiento caótico está muy lejos de ser totalmente desordenado y por el contrario, exhibe una estructura definida que resulta de pronto aparente. Otro aspecto del caos, es su extrema sensibilidad a las condiciones iniciales. Movimiento armónico simple M.A.S trata del ángulo que representa el estado inicial de vibración, es decir, la posición x del cuerpo en el instante t = 0. Su valor depende de si has elegido un seno o un coseno para representar el movimiento. una partícula se mueve ajo largo del eje x se dice que lo hace con un movimiento armónico simple cuando x, su desplazamiento desde el punto de equilibrio, varía en el tiempo de acuerdo con la relación x =Acos (ωt+φ) (13.1) donde A, ω, y φ son constantes del movimiento. Con el fin de brindar significado físico a estas constantes es conveniente graficar x como una función de t, de tal manera indicada en la figura. Observe primero que A, o amplitud del movimiento, es el desplazamiento máximo de la partícula en la dirección x, ya sea positiva o negativa. El ángulo constante φ recibe el nombre de constante de fase (o ángulo de fase) y junto con la amplitud A está determinado sólo por el desplazamiento y la velocidad inicial de la partícula. Las constantes φ y A nos indican cuál en el desplazamiento en el tiempo t=0. La cantidad (ωt+φ) es conocida como fase del movimiento y es útil para comparar los movimientos de dos sistemas de partículas. Advierta que la función x es periódica y se repite a si misma cuando ωt aumenta en 2 rad. El periodo, T, del movimiento es el tiempo que tarda la partícula en completar un ciclo. Es decir, el valor de x en un tiempo t es igual al valor de x en un tiempo t =2/ω con el hecho de que la fase aumenta en 2 rad en un tiempo T: Existen otros tipos de movimientos Movimiento periódico aquel que se repite cada intervalo fijo de tiempo. El ejemplo más sencillo es el movimiento circular uniforme que ya estudiamos en 4º de ESO. Se denomina período al tiempo que tarda en producirse una oscilación completa, al tiempo que tarda en repetirse el movimiento. Movimiento vibratorio es el movimiento periódico en el que el móvil oscila en torno a una posición de equilibrio estable moviéndose entre dos posiciones extremas. En toda oscilación mecánica intervienen dos factores: Una fuerza que está dirigida siempre hacia la posición de equilibrio, Movimientos circulares uniformes, como el de la punta de la aguja de un reloj. - Movimiento de un péndulo. - Movimiento de vibración de la membrana de un tambor. de una posición de equilibrio estable. Movimiento oscilatorio es un movimiento en torno a un punto de equilibrio estable. Este puede ser simple o completo. -Los puntos de equilibrio mecánico son, en general, aquellos en los cuales la fuerza neta que actúa sobre la partícula es cero, cuando una partícula, en un movimiento periódico, se mueve a lo largo de una misma trayectoria de ida y vuelta respecto a una posición de equilibrio, se dice que el movimiento que efectúa es oscilatorio o vibratorio
după JhonMV00 JhonMV00



