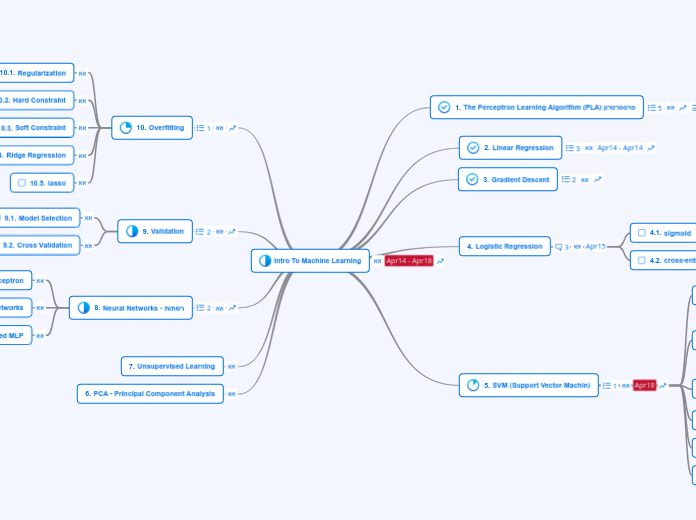
Intro To Machine Learning

Mai multe ca aceasta

Internet-based Project work

după claudia rivera

pschology teachers_theories

după B Carron

Accelerated Training

după Frank Mrosk

Fostering Software Craftsmanship

după Paweł Badeński

סיכומי שיעורים

קובץ תכנון למידה למבחן

Online Latex Editor

שיעורים

Intro To Machine Learning

PCA - Principal Component Analysis

Unsupervised Learning

Neural Networks - רשתות

Gradient Decent

Variable Learning Rate Gradient Descent

Stochastic (Online, Sequential) Gradient Descent

Propagation

Back Propagation

Forward Propagation

NN softened MLP

Sigmoidal Neural Networks

Multi-layer Perceptron

Validation

K-fold cross validation

Leave one out

Cross Validation

Model Selection

Overfitting

Ridge VS lasso

lasso

Ridge Regression

Soft Constraint

Hard Constraint

Regularization

SVM (Support Vector Machin)

Kernel Trick

KKT

Complementary Slackness

The Lagrange Dual Problem

The Lagrange Dual Function

Duality

Strong Duality

Weak Duality

Quadratic Programming

Hyperplanes

Margin of a Hyperplane

Soft-Margin SVM

Hard Margin SVM

The Maximum-Margin Separating Hyperplane

Spearating Hyperplane

Logistic Regression

Linear Regression

$h_w(x)=W^Tx$

The Normal Form

$X^T(y-X*W)=0$

convex

$e=(y-X*W)$

$E_{in}=\frac{1}{N}||e||^2$

cross-entropy error measure

sigmoid

Gradient Descent

מציאת מינימום בשיטה איטרטיבית

נצמצם כל צעד בקצת

רלוונטי להכל

Linear Regression

Least-Squeares Deriviation

Squared Loss Function

The Loss Function

The Perceptron Learning Algorithm (PLA) פרספרטרון

$\large (\sum_{i=1}^{d}w_ix_i) + b$

convex

הדאטא תמיד נמצא בחלק הפנימי של צורה כלשהי

• תמיד מתכנס

concave

הדאטא נמצא תמיד מחוץ לצורה כלשהיא

Non-Linearly Separable Data

דאטא שלא ניתן להפריד בצורה לינארית

The Pocket Algorithm

• אלגוריתם ששומר את ההתקדמות בכל שלב על מנת למצוא התכנסות
• תמיד יעצור בסוף
• יקר
• הרבה חישובים
• מבצע BackTracking

hyperplane

המישור המפריד בין חלקי הדאטא הניתנים להפרדה בצורה לינארית