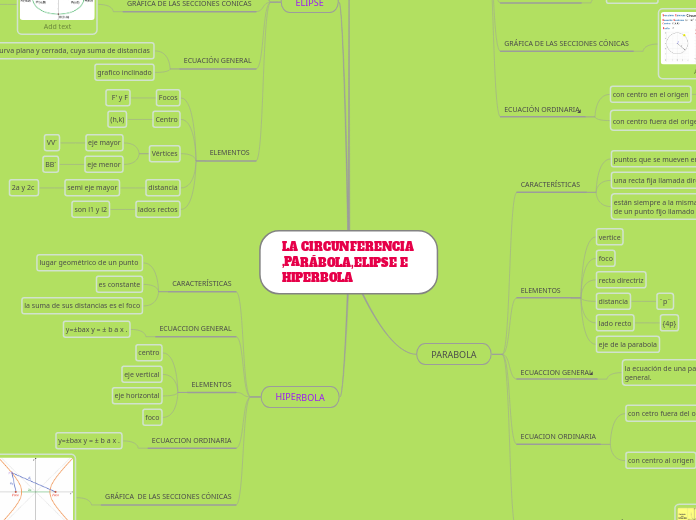
LA CIRCUNFERENCIA ,PARÁBOLA,ELIPSE E HIPERBOLA

Mai multe ca aceasta

Potencial de membrana en reposo

după Nicolle Arevalo

FUNCIÓN CUADRÁTICA

după Eliana Rojas

Secciones Conicas

după Geraldine Roman

DIFERENTES CONICAS

după Yilberto Trujillo Cetina

LA CIRCUNFERENCIA ,PARÁBOLA,ELIPSE E HIPERBOLA

HIPERBOLA

GRÁFICA DE LAS SECCIONES CÓNICAS

ECUACCION ORDINARIA

eje horizontal

eje vertical

centro

y=±bax y = ± b a x .

la suma de sus distancias es el foco

es constante

lugar geométrico de un punto

ELIPSE

lados rectos

son l1 y l2

semi eje mayor

2a y 2c

Vértices

eje menor

BB´

eje mayor

VV´

Centro

(h,k)

Focos

F' y F

grafico inclinado

curva plana y cerrada, cuya suma de distancias

ECUACIÓN ORDINARIA

focos paralelos al eje x

con centro fuera del origen

focos paralelos al eje y

lugar geométrico de un punto

suma de las distancias a dos puntos fijos

es una cantidad constante

se mueve en el plano cartesiano

PARABOLA

GRAFICA DE LAS SECCIONES CÓNICAS

ECUACION ORDINARIA

con centro al origen

gráfico horizontal

con centro en x

con cetro fuera del origen

gráfico vertical

con centro en y

ECUACCION GENERAL

la ecuación de una parábola horizontal en su forma general.

ELEMENTOS

eje de la parabola

lado recto

{4p}

distancia

¨p¨

recta directriz

foco

vertice

CARACTERÍSTICAS

están siempre a la misma distancia de un punto fijo llamado foco

una recta fija llamada directriz

puntos que se mueven en el plano

LA CIRCUNFERENCIA

ECUACIÓN ORDINARIA

con centro fuera del origen

cualquier coordenada menos 0,0

con centro en el origen

coordenadas son 0,0

GRÁFICA DE LAS SECCIONES CÓNICAS

Add text

ECUACIÓN GENERAL

IGUAL A CERO

ELEMENTOS

Radio de la circunferencia

Diámetro

punto de tangencia

secante

cuerda

diametro

radio

Centro

CARACTERÍSTICAS

punto fijo llamado centro de la circunferencia

tienen la misma distancia

son todos los puntos del plano.