Логарифми
У 1614 році шотландський математик-аматор Джон Непер опублікував на латинській мові твір під назвою «Опис дивовижної таблиці логарифмів». Термін логарифм, запропонований Непером, утвердився в науці.Логарифмом додаткового числа b за основою а (a>0, a≠0) називається ступінь показника, до якого необхідно піднести, щоб одержати і позначити log a b.
Нерівності
Логарифмічні нерівності - це нерівності, що містять змінну під знаком логарифма.При розв'язанні логарифмічних нерівностей пам'ятаємо:загальні властивості нерівностей;властивість монотонності логарифмічної функції;область визначення логарифмічної функції.
a
Схема
Розв'язування
Приклади

Функція
Логарифмічною функцією називається функція вигляду y=log a x, де a>0, a≠0. Множина значення логарифмічної функції — множина R усіх дійсних чисел.Властивість логарифмічної функціїВизначення області: D(y): x ϵ (0; +∞).Область значень: E(y): y ϵ (-∞;+∞).Парність / непарність: функція ні парна, ні непарнаЕкстремумні функції: функція не має екстремумів.

Графіки
Властивості
Приклади

Музика
Саме Піфагор створив першу математичну теорію музики, і хоча музиканти не дуже люблять перевіряти „алгеброю гармонію”, вони весь час мають справу з математикою, бо сучасна гама обґрунтовується на логарифмах. Будемо називати найнижчу октаву нульовою; кількість коливань ноти до цієї октави за 1 секунду використовуємо за 1.Тоді ноти до першої октави буде робитися на два рази більше коливань. Позначимо всі ноти хроматичної гами номерами р , приймаючи за нульовий перший тон кожної гами. Тоді тон сол буде 7-й, ля -9-й, 12-й тон буде робити знову, тільки октавою вище.
a
Піфагор
Піфагор був не тільки великим математиком, а й хорошим музикантом. Він встановив, що приємні сполучення звуків відповідають певному складу між довгою струною, що коливаються, або відстаням між дірочками сопілки. Саме він створив першу математичну теорію музики, і хоча музиканти не дуже люблять перевіряти „алгебру гармонію”, вони весь час мають справу з математикою, бо сьогодні гама обґрунтовується на логарифмах.

"Граючи на клавішах сучасного роялю, музикант, чесно кажучи, грає на логарифмах"

Леонард Ейлер
Властивості
Основні властивості логарифмів:Логарифм одиниці за будь-якою основою дорівнює нулю.Логарифм добутку додатних чисел дорівнює сумі логарифмів множників.Логарифм частки додатних чисел дорівнює різниці логарифмів діленого і дільника.Логарифм степеня додатного числа дорівнює добуткові показника степеня на логарифм основи цього степеня.

Формули
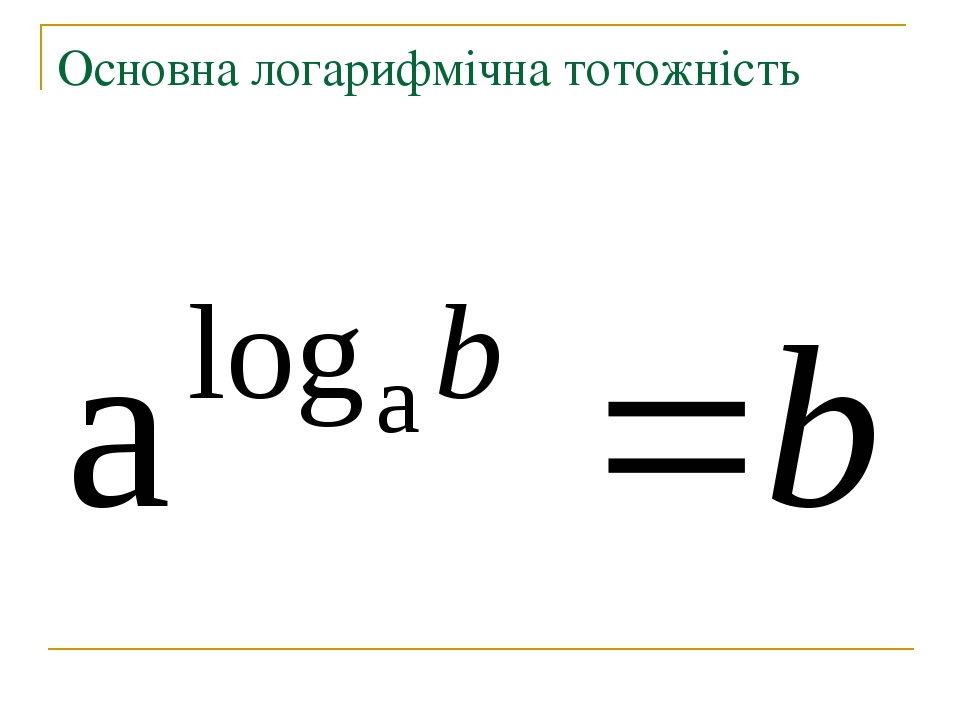
Тотожність
Властивості

Рівняння
Логарифмічними засобами рівняння , які складаються зі зміною під знаком логарифма. Розв'язати логарифмічне рівняння – це означає знайти всі його корені або довести, що рівняння коренів не має.Основні методи розв'язування логарифмічних рівнів:Метод зведення логарифмічного рівня до алгебраїчного.Метод потенціювання. Метод зведення логарифмів до однієї основи.Метод логарифмування.Графічний метод розв'язування логарифмічних рівнів.
aРозв'язування

Типи
Приклади

Логарифми в житті людини
Логарифмічна функція запускається у зв'язку з найрізноманітнішими природними формами. По логарифмічних спіралях розташовуються квітки в суцвіттях соняшника, закручуються раковини молюска Nautilus, роги гірського барану і дзьоби папуг. Один із павуків, епейра, розплітаючи павутиння , закручує нітки навколо центру по логарифмічним спіралям.

Логарифмічна спіраль

Павутина

Приклади