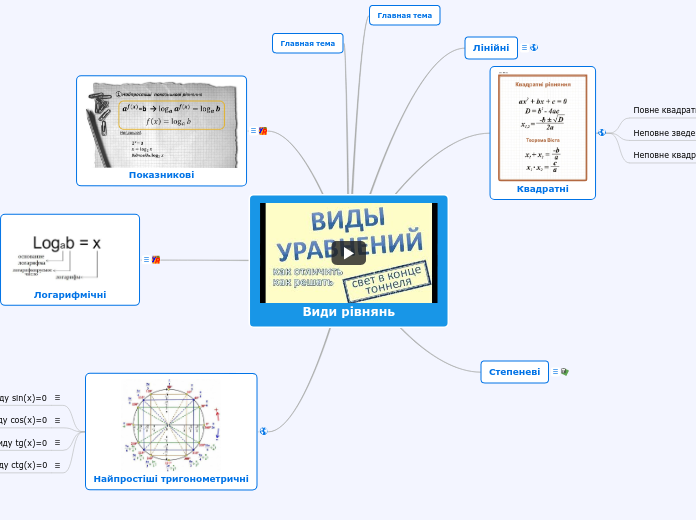
Види рівнянь

Лінійні рівнянняОзначення. Рівняння виду ax+b=0 називаються лінійними.Якщо a\neq 0 , то x=\frac{-b}{a} - єдиний корінь;Якщо a=0 , b=0 , то коренем рівняння буде будь-яке дійсне число;Якщо a=0 , b\neq 0 , то рівняння не має коренів.

Квадратні рівняння (повні)Означення. Рівняння виду ax^2+bx+c=0 називається повним квадратним рівнянням.D=b^2-4ac .якщо D\geq 0 , то рівняння два дійсні корені:x_{1,2}=\dfrac{-b\pm \sqrt{D}}{2a}.якщо D<0 , то рівняння не має коренів.

Квадратні рівняння (неповні зведені)Означення. Рівняння виду x^2+px+q=0 називається неповним зведеним квадратним рівнянням.За теоремою Вієта:x_1+x_2=-p; x_1\cdot x_2=q .

Квадратні рівняння (неповні)Означення. Якщо для рівняння видуx^2+px+q=0: q=0 або p=0, то таке рівняння називається неповним квадратним рівнянням.x^2+px=0 ;x^2+q=0.

Степеневі рівнянняПросте степеневе рівняння x^{n}=a при різних значеннях n і a (n - натуральне число):при будь-якому додатному a рівнянняx^n=a має єдиний дійний коріньx=\sqrt[n]{a}, якщо число n непарне або два дійсних корені x=\pm \sqrt[n]{a} , якщо число n парне;при a=0 рівняння x^n=a має тільки один корінь: x=0 ;при будь-якому від’ємному a рівнянняx^n=a має єдиний дійсний коріньx=\sqrt[n]{a} , якщо n непапне і не має жодного дійсного кореня, якщо n парне.

Показникові рівнянняОзначення. Рівняння виду a^{x}=b , де a>0 називається показниковим рівнянням.Методи розв’язування простих показникових рівняньПорівняння основ:\left( a^n=a^m, a>0 \right) \Leftrightarrow x=m; Якщо основи рівні, то і показники рівні.Порівняння показників:\left(x^b=y^b, b>0 \right) \Leftrightarrow x=y; Якщо показники рівні, то і основи рівні.За означенням степенів:\left( a^x=b, a>0, b>0 \right) \Leftrightarrow x=\log_{a}{b} .

Логарифмічні рівнянняОзначення. Логарифмічне рівняння — рівняння, в якому змінна знаходиться під знаком логарифма.log_{a}{x}=c, log_{x}{b}=c, a>0, b>0.Якщо a<0, рівняння не має розв’язку.Методи розв’язання простих логарифмічних рівняньЗа означенням: \left( log_{a}{x}, a>0 \right) \Leftrightarrow a^c=x;За порівнянням: \left( \log_{a}{x}=\log_{a}{b}, a>0, b>0 \right) \Leftrightarrow x=b.

Найпростіші тригонометричні рівняння\sin{x}=a: -1\leq a\leq 1; x=\left(-1\right)^{n}\arcsin{a}+\pi{n}, n\in \mathbb{Z}.

Найпростіші тригонометричні рівняння\cos{x}=a: -1\leq a\leq 1 ; x=\pm \arccos{a}+2\pi{n}, n\in \mathbb{Z}.

Найпростіші тригонометричні рівняння\tan{x}=a: x=\arctan{a}+\pi{n}, n\in \mathbb{Z}.

Найпростіші тригонометричні рівняння\cot{x}=a:x=arcctg\;a+\pi{n}, n\in \mathbb{Z}.