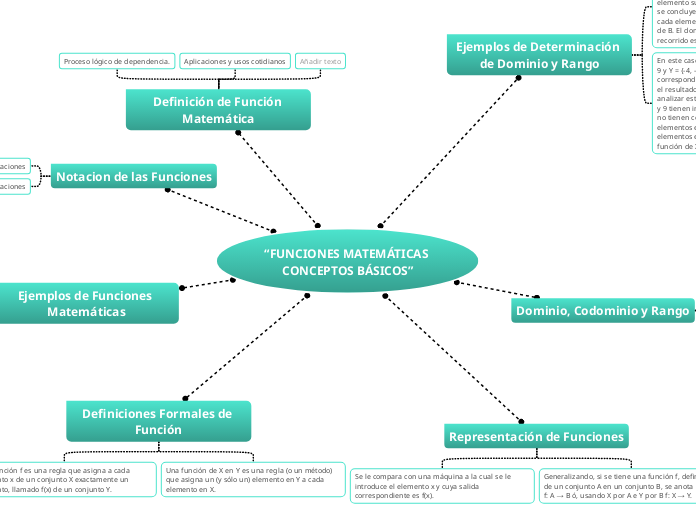
“FUNCIONES MATEMÁTICAS CONCEPTOS BÁSICOS”
Ejemplos de Determinación de Dominio y Rango
El conjunto A contiene los elementos {1, 2, 3}, mientras que el conjunto B consiste en {0, 4, 6, 8, 10, 12}. La relación entre A y B es "asignar a cada elemento su cuádruplo". Al examinar esta relación, se concluye que es una función de A en B porque cada elemento de A se asigna a un único elemento de B. El dominio de esta función es {1, 2, 3}, y su recorrido es {4, 8, 12}.
En este caso, se tienen los conjuntos X = {-4, -1, 0, 4, 9 y Y = {-4, -3, -2, -1, 0, 1, 2, 3, 4\}. La regla de correspondencia es "asignar a cada elemento de X el resultado de extraer su raíz cuadrada". Al analizar esta regla, se observa que los números 0, 4 y 9 tienen imágenes en Y, pero los números -4 y -1 no tienen correspondencia en Y. Dado que hay elementos en X que no se corresponden con elementos en Y, esta relación no constituye una función de X en Y .
Dominio, Codominio y Rango
Dominio: Conjunto de todos los posibles valores de entrada para los cuales la función está definida.
Codominio: Conjunto de todos los posibles valores de salida que la función puede producir.
Rango: Conjunto de valores reales que la función realmente produce cuando se evalúa sobre todos los posibles valores de entrada en el dominio. Puede ser un subconjunto del codominio.
Representación de Funciones
Se le compara con una máquina a la cual se le
introduce el elemento x y cuya salida correspondiente es f(x).
Generalizando, si se tiene una función f, definida de un conjunto A en un conjunto B, se anota
f: A → B ó, usando X por A e Y por B f: X → Y.
Definición de Función Matemática
Proceso lógico de dependencia.
Aplicaciones y usos cotidianos
Añadir texto
Notacion de las Funciones
Reglas de las notaciones
Función y uso de las notaciones
Ejemplos de Funciones Matemáticas
La regla de "elevar al cuadrado": f(x)=X²
la regla "doble del número más 3".
x →2x + 3
Correspondencia entre las personas que trabajan en una oficina y su peso
Definiciones Formales de Función
Una función f es una regla que asigna a cada elemento x de un conjunto X exactamente un elemento, llamado f(x) de un conjunto Y.
Una función de X en Y es una regla (o un método) que asigna un (y sólo un) elemento en Y a cada elemento en X.