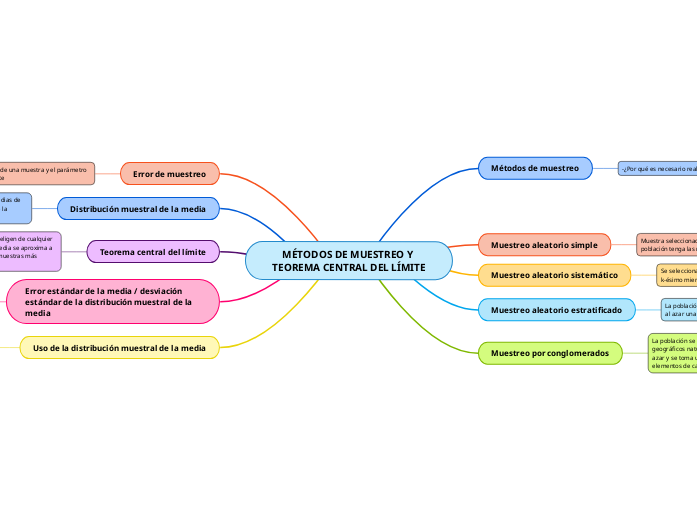
MÉTODOS DE MUESTREO Y TEOREMA CENTRAL DEL LÍMITE

-¿Por qué es necesario realizar un muestreo?

Establecer contacto con la población en menos tiempo

Para que el costo de estudiar los elementos de una población sea más bajo

Lograr identificar todos los elementos de una población de manera aproximada

Que no haya riesgo de perder la vida al hacer pruebas

El resultado del muestreo sea adecuado

Muestra seleccionada de manera que cada elemento de la población tenga las mismas posibilidades de que se incluya

Sorteo, profesor formando equipos, o en este caso eligiendo alumnos para exponer, etc.

Se selecciona un punto aleatorio de inicio y luego se elige cada k-ésimo miembro de la población

Selección de días de la semana, horarios, etc.

La población se divide en subgrupos (estratos) y se selecciona al azar una muestra de cada uno

Dividir alumnos que sacaron de 90-100, 80-90, 70-80, de promedio el semestre pasado, se elige uno de cada subgrupo y hacer la investigación que se requiera.

La población se divide en conglomerados a partir de los límites geográficos naturales u otra clase. Después se seleccionan al azar y se toma una muestra de manera aleatoria con elementos de cada grupo.

Estudio de mercado. Un área geográfica extensa puede ser costosa de estudiar.

Diferencia entre el estadístico de una muestra y el parámetro de la población correspondiente

Distribución de probabilidad de todas las posibles medias de las muestras de un determinado tamaño muestral de la población.

Si todas las muestras de cierto tamaño se eligen de cualquier población, la distribución muestral de la media se aproxima a una distribución normal, esta mejora con muestras más grandes

Mide la variación de la distribución muestral de las medias. Se puede decir que es un margen de error

Si la población se rige por una distribución normal, la distribución muestral de la media también se regirá por la distribución normal con muestras de cualquier tamaño.