Las Figuras Cónicas.
¿Qué son?
Se le denominan secciones cónicas a todas las figuras y curvas formadas al hacer un corte con un plano sobre un cono circular recto.
Formas de las conicas
¿De dónde surgen?
El matemático griego Menecmo descubrió estas curvas y fue el matemático griego Apolonio de Perga el primero en estudiar detalladamente las curvas cónicas y encontrar la propiedad plana que las definía. Apolonio descubrió que las cónicas se podían clasificar en tres tipos a los que dio el nombre de: elipses, hipérbolas y parábolas.
Circunferencia
Es el lugar geométrico de los puntos del plano cuya distancia a un punto fijo, denominado centro, es constante.
La circunferencia se forma cuando el corte del eje es paralelo a la base.

Forma de la circunferencia.
Para todas las secciones se cumple la ecuación general: Ax^2+Cy^2+Dx+Ey+F=0
La condición para que la ecuación propuesta sea circunferencia es que A sea igual a C, en cuanto a signos y números respecta.
La ecuación canónica de la circunferencia es:
(x-h)^2+(y-k)^2 = r^2.
Donde el centro de la circunferencia es determinado por (h,k) y el r es el radio (al que se le debe sacar raíz cuadrada).
¿Cómo pasar de la ecuación canónica a la general?
Primer paso: Tenemos la ecuación canónica de la circunferencia que es: (x - α)^2 + (y - β)^2 = r^2
Segundo paso: Donde observamos dos trinomios cuadrados perfectos y debemos resolverlo de la siguiente manera:
x^2 - 2*a*x + α^2 + y^2 - 2*β*y + β^2 = r^2
Tercer paso: Se reagrupan los términos y queda de la siguiente manera:
x^2 + y^2 - 2*a*x - 2*β*y + (α^2 + y^2 + β^2) = r^2
Cuarto paso: Y renombramos las constantes:
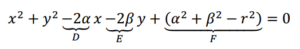
Constantes renombradas.
Quinto paso: Se obtiene la ecuación:
x^2 + y^2 + Dx + Ey + F = 0
¿Cómo pasar de la ecuación general a la canónica?
Primer paso: Debemos ordenar la ecuación general uniendo las x´s y las y´s. De la siguiente manera: Ax^2+Dx+?+Cy^2+Ey+¿=F
Segundo paso: Ahora debemos encontrar el tercer término de cada trinomio, con la ecuación (b/2)^2, de la siguiente manera:
{Ax^2+Dx + (b/2)^2}+{Cy^2+Ey+(b´/2)^2}=F +(b/2)^2+
(b´/2)^2
De esta manera se forman los Trinomios Cuadrados Perfectos.
Tercer paso: Transformar el TCP a binomio al cuadrado, De la siguiente forma: (x-h)^2+(y-k)^2=F+(b/2)^2+ (b´/2)^2
Cuarto paso: De esta forma se transforma en la ecuación canónica que es:
(x-h)^2+(y-k)^2 = r^2.
¿Cuáles son sus aplicaciones?
Se utilizan técnicas circunferenciales para muchas cosas hoy en día, por ejemplo los CD's que aunque parezcan piezas ordinarias, en la música actual requieren de mucha precisión para su correcto funcionamiento. Por lo tanto para su fabricación se utilizan las técnicas del radio y del diámetro.
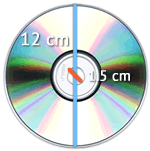
La circunferencia de un CD.
En otros aspectos de la vida en que se presencia notoriamente el uso de las circunferencias es en el transporte: principalmente en las ruedas y un ejemplo claro es en la bicicleta, un conjunto de tubos metálicos con dos ruedas que aplican la geometría perfectamente: las ruedas están hechas de un “arco” . La parte más interesante de esto es que la rueda se afirma desde el centro y desde este salen un montón de alambres delgados llamados “rayos” y estos son radios que mantienen la forma circunferencial de la rueda perfectamente.
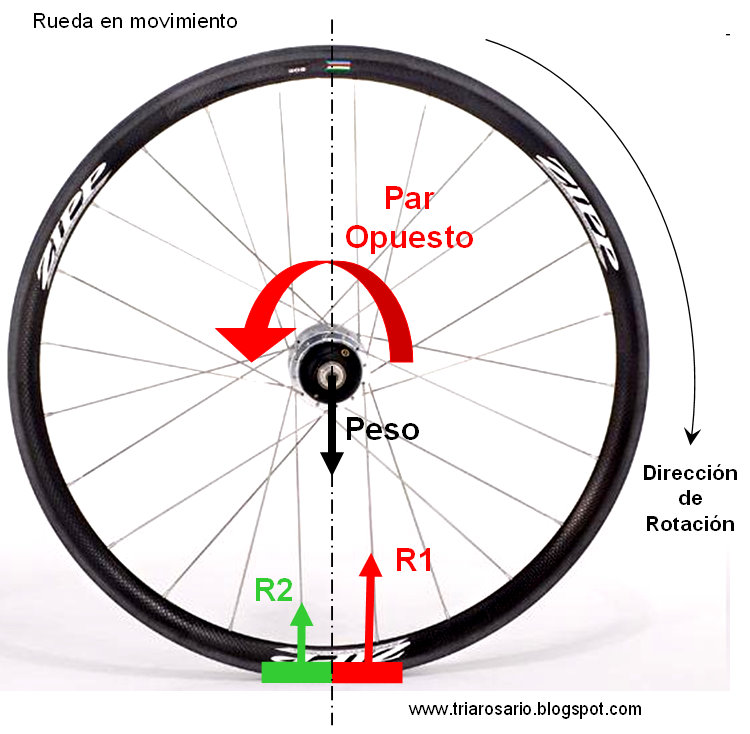
La circunferencia de la rueda de una bicicleta.
WEBGRAFÍA:
Natalia (27/09/2009) "El mundo de las circunferencias"
Recuperado de: http://circunseis.blogspot.com/2009/09/la-circunferencia-es-uno-de-los.html
Elipse
Es el lugar geometrico de los puntos de un plano en el que la suma de las distancias a otros dos puntos fijos llamados focos es cosntante. Es la curva simetrica cerrada que resulta al cortar la superficie de un cono por un plano oblicuo al eje de simetria.
La Elipse se genera cuando el plano α es oblicuo respecto al eje, y corta a todas las generatrices.

Forma de la elipse.
Para todas las secciones se cumple la ecuación general: Ax^2+Cy^2+Dx+Ey+F=0
La condición para que la ecuación propuesta sea elipse es que A y C tengan el mismo signo pero deben ser distintos números.
¿Cuáles son sus aplicaciones?
Las órbitas de los planetas alrededor del sol son elípticas (el sol se encuentra en uno de los focos). La excentricidad de la órbita de la Tierra alrededor del Sol es aproximadamente 0,0167.

Las órbitas de los planetas alrededor del sol
En arquitectura se utilizan con mayor frecuencia arcos con forma elíptica. Además existen capillas o galerías de los secretos. Son estructuras con techos elipsoidales los cuales permiten que se pueda oir a una persona que está en un foco desde el otro foco y las personas que están entre las otras dos no oirán nada.
Arquitectura
WEBGRAFÍA:
1. Suárez, L (12/08/2014) Cónicas: En la vida real.
Recuperado de: https://liyuansuarez.jimdofree.com/2014/08/12/c%C3%B3nicas-en-la-vida-real/
2. Anónimo (2016) Elipse.
Recuperado de: http://quiz.uprm.edu/pc_cb/elipse/elipse_traslada.html#:~:text=Algunas%20aplicaciones%2C%20curiosidades%20y%20utilidades,1.&text=En%20arquitectura%20se%20utilizan%20con,o%20galer%C3%ADas%20de%20los%20secretos
Hipérbola
Es el lugar geométrico de los puntos del plano en el que la diferencia de distancias a dos puntos fijos denominados focos, F y F', es siempre constante.
La Hipérbola se genera cuando el plano a es paralelo a dos generatrices. Por cuestiones didácticas y de mejor comprensión, se suele representar utilizando un plano a paralelo al eje de la superficie cónica de revolución.
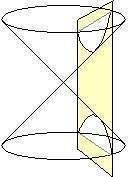
Forma de la hipérbola.
Para todas las secciones se cumple la ecuación general: Ax^2+Cy^2+Dx+Ey+F=0
La condición para que la ecuación propuesta sea una elipse es que A y C tengan signos y números diferentes.
¿Cuáles son sus aplicaciones?
El cálculo de cuerpos celestes ajenos al sistema solar que entren en él, atraídos por el sol describen una trayectoria en forma de hipérbola, por lo que puede ser calculado su camino con toda precisión.
Cuerpos celestes y la hipérbola que los conforma.
Algunos cometas que no tienen un ciclo periódico presentan una trayectoria en forma de hipérbola cuando se acercan al sol.
WEBGRAFÍA:
Anónimo (09/2020) 10 usos de la hipérbola.
Recuperado de: https://10ejemplos.com/10-ejemplos-de-hiperbola/
Parábola
Es el lugar geométrico de los puntos de un plano que tienen equidistancia respecto a un punto fijo y una recta. Este lugar se crea a partir de la acción de un plano que es paralelo a la generatriz y que disecciona un cono circular.
La Parábola se genera cuando el plano a es paralelo a una generatriz.
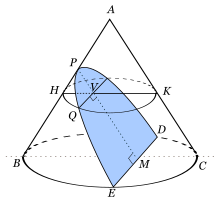
Forma de la parábola.
Para todas las secciones se cumple la ecuación general: Ax^2+Cy^2+Dx+Ey+F=0
La condición para que la ecuación propuesta sea parábola es que sólo exista x^2 o y^2, más no ambas. Es decir que A o C sea igual a 0.
¿Cuáles son sus aplicaciones?
Las trayectorias de los proyectiles tienen forma parabólica. Los chorros de agua que salen de un surtidor tienen también forma parabólica.

Proyectiles y parábolas.
La forma de los telescopios, detectores de radar y reflectores luminosos son parabólicas. En los faros de los coches se coloca la fuente de luz en el foco de la parábola, de modo que los rayos, al reflejarse en la lámpara, salen formando rayos paralelos.

Telescopios y las parábolas.
WEBGRAFÍA:
Suárez, L (2014) Cónicas en la vida real. Recuperado de:https://liyuansuarez.jimdofree.com/2014/08/12/c%C3%B3nicas-en-la-vida-real/
