PARABOLA
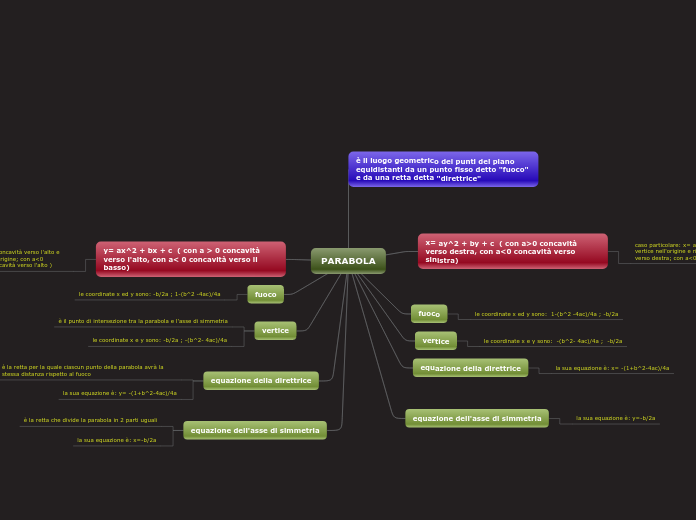
è il luogo geometrico dei punti del piano equidistanti da un punto fisso detto "fuoco" e da una retta detta "direttrice"
x= ay^2 + by + c ( con a>0 concavità verso destra, con a<0 concavità verso sinistra)
caso particolare: x= ay^2 (con a=1 asse dato dalle ascisse, vertice nell'origine e rivolto verso destra; con a>0 concavità verso destra; con a<0 concavità verso sinistra)
fuoco
le coordinate x ed y sono: 1-(b^2 -4ac)/4a ; -b/2a
vertice
le coordinate x e y sono: -(b^2- 4ac)/4a ; -b/2a
equazione della direttrice
la sua equazione è: x= -(1+b^2-4ac)/4a
equazione dell'asse di simmetria
la sua equazione è: y=-b/2a
y= ax^2 + bx + c ( con a > 0 concavità verso l'alto, con a< 0 concavità verso il basso)
caso particolare: y=ax^2 ( con a=1 concavità verso l'alto e con asse delle ordinate e vertice nell'origine; con a<0 concavità verso il basso; con a>0 concavità verso l'alto )
fuoco
le coordinate x ed y sono: -b/2a ; 1-(b^2 -4ac)/4a
vertice
è il punto di intersezione tra la parabola e l'asse di simmetria
le coordinate x e y sono: -b/2a ; -(b^2- 4ac)/4a
equazione della direttrice
è la retta per la quale ciascun punto della parabola avrà la stessa distanza rispetto al fuoco
la sua equazione è: y= -(1+b^2-4ac)/4a
equazione dell'asse di simmetria
è la retta che divide la parabola in 2 parti uguali
la sua equazione è: x=-b/2a