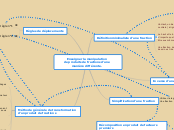
Enseigner la manipulation
de produits de fractions d'une manière différente.
Définition minimaliste d'une fraction
Un Haut, un bas, les deux séparés par une barre centrale ( alignée sur la ligne d'écriture)
Le haut et le bas sont des nombres écrits sous n'importe quelle forme (explicite ou littéral) et peuvent être eux même des fractions.
Une fraction dont le haut et le bas sont le même dessin est identique à l'unité.
Inverse d'une fraction
Savoir identifier la barre centrale d'une fraction
Écrire la barre centrale sur la ligne d'écriture
Simplification d'une fraction
Utiliser la règle 2 pour faire apparaitre
Une fraction identique à l'unité.
Règles de déplacements
Règle n°1
Le haut j'y touche pas,
le bas je l'inverse
Règle n°2
Je multiplie les hauts ensembles
et les bas ensembles
Méthode générale de transformation
d'un produit de fractions
Pourcentages
Mise au même dénominateur
Comparaison de fractions
Somme de fractions
Calcul de produits de quotients de fractions contenant des nombres non fractionnaires ou des fractions sous forme explicite ou littérale.
Résolution de situations de proportionnalité impliquant des grandeurs.
Conversions d'unités quotient/produit
Calcul littéral impliquant des fractions
Décomposition en produit de facteurs premiers
Divisibilité/Multiple
Division
Nombre entier
Multiplication