RULES OF DIFFERENTIATION
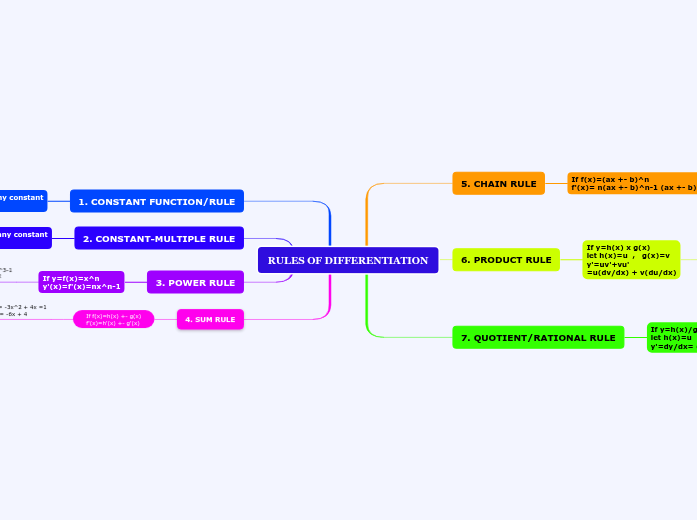
5. CHAIN RULE
If f(x)=(ax +- b)^n
f'(x)= n(ax +- b)^n-1 (ax +- b)
f(x)=(3x-2)^5
f'(x)=5(3x-2)^4 (3x-2)
f'(x)=5(3x-2)^4 (3)
f'(x)=15(3x-2)^4
6. PRODUCT RULE
If y=h(x) x g(x)
let h(x)=u , g(x)=v
y'=uv'+vu'
=u(dv/dx) + v(du/dx)
f(x)=(4x-5)(-2x^2 + 3)
u' = 4
v' = -4x
so ;
f'(x) = uv' + vu'
f'(x)=(4x-5)(-4x)+((-2x^2)+3)(4)
= -16x^2 + 20x - 8x^2 + 12
= -24x^2 + 20x + 12
7. QUOTIENT/RATIONAL RULE
If y=h(x)/g(x)
let h(x)=u , g(x)=v
y'=dy/dx= (vu'-uv')/v^2
f(x)=3x/(2x+1)
u' = 3
v' = 2
so ;
f'(x)=[(2x+1)3 - 3x(2)] / (2x+1)^2
=(6x+3-6x) / (2x+1)^2
=3/(2x+1)^2
1. CONSTANT FUNCTION/RULE
if y=f(x)=c , where c is any constant
dy/dx=f'(x)=0
If f(x)=4
f(x)=0
2. CONSTANT-MULTIPLE RULE
If f(x)=mx , where m is any constant
f'(x)=dy/dx=m
If f(x)=5x
f'(x)=5
3. POWER RULE
If y=f(x)=x^n
y'(x)=f'(x)=nx^n-1
f(x)=5x^3
f'(x)=(3)5x^3-1
f'(x)=15x^2
4. SUM RULE
If f(x)=h(x) +- g(x)
f'(x)=h'(x) +- g'(x)
f(x)= -3x^2 + 4x =1
f'(x)= -6x + 4