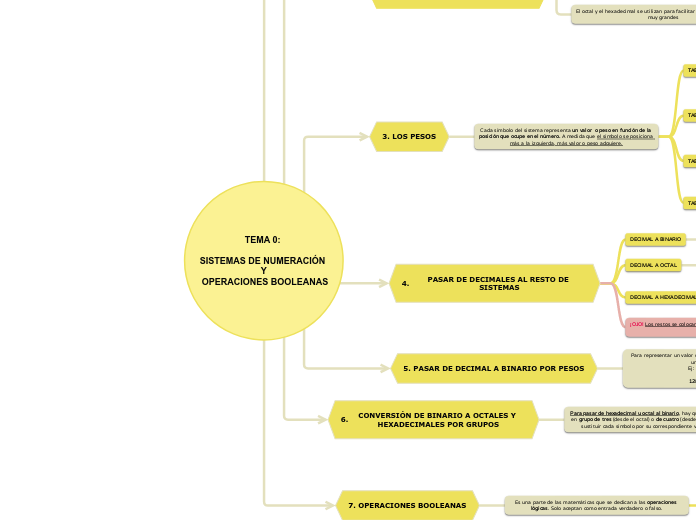
TEMA 0:
SISTEMAS DE NUMERACIÓN
Y
OPERACIONES BOOLEANAS
LOS SÍMBOLOS
BINARIO
BASE 2
0 y 1
OCTALES
BASE 8
0,1,2,3,4,5,6 y 7
DECIMALES
BASE 10
0, 1, 2, 3, 4, 5, 6, 7, 8 y 9
HEXADECIMALES
BASE 16
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
¿Cuándo se utilizan las letras?
Cuando nos quedamos sin números más allá del 9
Así, la A representa nuestro 10, la B al 11, la C al 12, la D al 13, la E al 14 y la F al 15
¿POR QUÉ SE UTILIZAN BINARIOS?
En los sistemas informáticos utilizamos el binario porque son los dos estados que maneja la máquina. En un ordenador, los datos se almacenan en binario
Los binarios sirven para dejar pasar o no la corriente dentro de un sistema informático y los procesadores son los que van a leer las instrucciones en binario.
El octal y el hexadecimal se utilizan para facilitar el manejo de números muy grandes
¿Qué tienen en común el sistema binario, octal y hexadecimal?
Los tres sistemas tienen una base múltiplo de dos:
∙ Binario, con base 2 = 2^1
∙ Octal, con base 8 = 2^3
∙ Hexadecimal, con base 16 = 2^4
LOS PESOS
Cada símbolo del sistema representa un valor o peso en función de la posición que ocupe en el número. A medida que el símbolo se posiciona más a la izquierda, más valor o peso adquiere.
TABLA SISTEMA DECIMAL
6 5 4 3 2 1 0 POSICIÓN
10^6 10^5 10^4 10^3 10^2 10^1 10^0 POTENCIAS
1000000 100000 10000 1000 100 10 1 PESOS
TABLA SISTEMA BINARIO
6 5 4 3 2 1 0 POSICIÓN
2^6 2^5 2^4 2^3 2^2 2^1 2^0 POTENCIAS
64 32 16 8 4 2 1 PESOS
TABLA SISTEMA OCTAL
6 5 4 3 2 1 0 POSICIÓN
8^6 8^5 8^4 8^3 8^2 8^1 8^0 POTENCIAS
262.144 32.768 4.096 512 64 8 1 PESOS
TABLA SISTEMA HEXADECIMAL
4 3 2 1 0 POSICIÓN
16^4 16^3 16^2 16^1 16^0 POTENCIAS
65536 4096 256 16 1 PESOS
PASAR DE DECIMALES AL RESTO DE SISTEMAS
DECIMAL A BINARIO
Dividimos consecutivamente por 2, obteniendo como restos 0 y 1.
DECIMAL A OCTAL
Dividimos consecutivamente por 8, obteniendo como restos símbolos menores que 8 (0..7)
DECIMAL A HEXADECIMAL
Dividimos consecutivamente por 16, obteniendo como restos números menores que 16 (0..15)
¡OJO!
Si el resto es un número mayor a 9,se debe sustituir por una letra.
EJEMPLO: 10=A, 11=B...
¡OJO! Los restos se colocan de abajo a arriba y en orden de izquierda a derecha
PASAR DE DECIMAL A BINARIO POR PESOS
Para representar un valor decimal en binario hay que desglosarlo en una tabla de pesos:
Ej: 128 (10= 1000000
128 64 32 16 8 4 2 1
Los pesos elegidos han de sumar el número decimal. Para hacerlo, ha de asignarle el mayor peso que “quepa”, y a continuación repetir la operación con lo que quede hasta completar la suma
CONVERSIÓN DE BINARIO A OCTALES Y HEXADECIMALES POR GRUPOS
Para pasar de hexadecimal u octal al binario, hay que hacerlo siempre en grupo de tres (desde el octal) o de cuatro (desde el hexadecimal) y sustituir cada símbolo por su correspondiente valor en binario
OPERACIONES BOOLEANAS
Es una parte de las matemáticas que se dedican a las operaciones lógicas. Solo aceptan como entrada verdadero o falso.
TIPOS DE BOOLEANOS
AND O Y
Tienen que tener verdadero las dos entradas para ser verdaderas, sino es falsa
OR U O
Con que una de las dos entradas sea verdadero, ya es verdadero
XOR U O
Debe aparecer en una de las dos entradas un verdadero. Han de ser verdad uno u(O) otro de forma EXCLUSIVA. En cual-
quier otro caso, el resultado es 0 (falso).
NOT
Lo contrario a lo que ponga la entrada