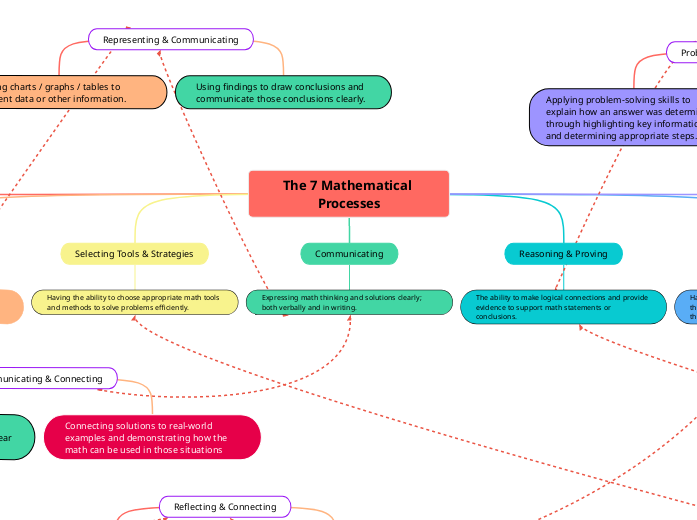
The 7 Mathematical Processes
Being able to recognize and make connections between different math concepts, representations, and problem-solving strategies.
The ability to express math ideas in a variety of ways, such as: numbers, symbols, diagrams, and models.
Selecting Tools & Strategies
Having the ability to choose appropriate math tools and methods to solve problems efficiently.
Expressing math thinking and solutions clearly; both verbally and in writing.
The ability to make logical connections and provide evidence to support math statements or conclusions.
Having the awareness to think about and consider the processes used, the strategies employed, and the solutions that were found.
The ability to find solutions to math challenges through trial and error of a variety of strategies and approaches.
Problem Solving & Reasoning
Applying problem-solving skills to explain how an answer was determined through highlighting key information and determining appropriate steps.
Justifying a chosen approach and explaining its validity.
Connecting & Representing
Using graphs / charts / pictures / diagrams / tables to connect how data is graphed or represented to specific math concepts.
Using different representations (i.e. tables / graphs / equations) to convey the same math relationships between numbers or information.
Communicating & Connecting
Arguing / supporting / being able to share solutions effectively by being clear and relating ideas verbally.
Connecting solutions to real-world examples and demonstrating how the math can be used in those situations
Representing & Communicating
Creating charts / graphs / tables to represent data or other information.
Using findings to draw conclusions and communicate those conclusions clearly.
Selecting Tools & Problem Solving
Selecting appropriate assistive technologies or methods to solve the specific problem at hand.
Determining the best approach to obtain accurate answers that best suits the needs of the problem.
Reflecting on the process of working through mathematical concepts before / during / after an activity and making connections to prior knowledge.
Recognizing similarities between current problems and previous ones - allowing for deeper understanding.
Being able to demonstrate and explain why solutions are correct.
Assessing how you arrived at an answer and evaluating alternative methods or potential mistakes.