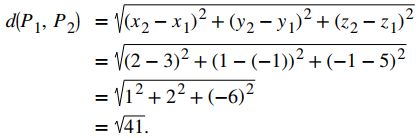Vectores

Vector unitario
Sólo indican dirección
Magnitud 1




Cálculo de aréas
Aréa de un Triángulo
Dados dos vectores que forman un triángulo, siendo estos dos de sus lados como se muestra en la imagen, la fórmula para obtener el área del triángulo es:


Aréa de un paralelogramo
Para calcular el área de un paralelogramo de vértices A, B, C y D hallamos los vectores no paralelos AB y AD.
El módulo del vector obtenido al hacer el producto vectorial, es el área del paralelogramo formado por los vectores no paralelos

Cálculo de Volumenes
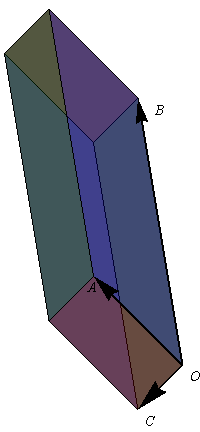
Tetraedro
Un tetraedro es un caso particular de pirámide. El volumen de una pirámide es 1/3 del volumen del prisma que tiene la misma base y la misma altura. Si tomamos como base el triángulo definido por O, A y B, la altura es la proyección de \overrightarrow{OC} en la dirección normal a la superficie


Paralelepípedo
El volumen de un paralelepípedo se calcula como el producto mixto (sin signo) de los tres vectores que definen el paralelepíedo.

Topic principal
Tipos de Vectores

Libres
Un vector es libre cuando su punto
de aplicacción es libre o no está definido.
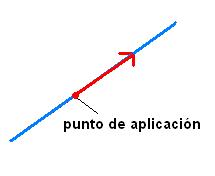
Se utiliza para nombar al lugar en el cual se aplica una fuerza

Fijos
Mismo modulo , dirección y sentido.

Ligados
Vectores que actuan en la misma recta
, misma dirección , sentido y modulo.

Opuestos
Dos vectores que comparten misma
magnitud y misma dirección pero con sentido opuesto

Concurrentes
Todos aquellos vectores
que atraviesan un mismo punto y dan
la creación de un angulo.
Sistema

Colineales
Todos aquellos vectores contenidos
en una sola linea de acción
Concurrentes
Características
Origen
Punto de Aplicación
Subtopic
Magnitud
Longitud o tamaño

2D: Ø=tan(a2/a1)
3D: û=(cos(alfa),cos(beta),cos(gamma))
Dirección
Orientación en el espacio

Sentido
Línea de acción donde se dirige

Denotación

v
Subindice superior compañado de una flecha
Negritas
Clasificación

Coplanares
Vectores encontrados en el mismo plano

No Coplanares
Vectores no encontrados en el mismo plano
Operaciones con Vectores
Suma
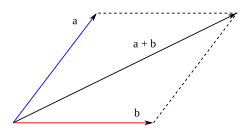
Método del paralelogramo
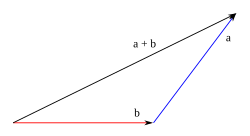
Método del triángulo
Resta

Producto
Producto escalar o producto punto
Producto vectorial o producto cruz
a X b
Propiedades
Si a, b y c son vectores y c es un escalar entonces:
a X b = -b X a
(ca) X b = c(a X b) = a X (cb)
a X (b + c) = a X b + a X c
(a + b) X c = a X c + b X c
a * (b X c) = (a X b) * c
a X (b X c) = (a * c)b - (a * b)c
Ángulo entre dos vectores

Descomposiciones de un vector

Propiedades de las operaciones
Suma de Vectores
a + b = b + a
Propiedad Conmutativa
a - b = b - a
Suma del opuesto
a + (b + c) = (a + b) + c
Propiedad Asociativa
a + 0 = a
Propiedad Identidad
a + (-a) = 0
si a, b, y c son vectores y c y d son escalares:
Producto escalar con vector
c (a) = c a
Propiedad Distributiva
c(a + b) = ca + cb
Propiedad Distributiva
(c + d)a = ca + da
Propiedad Dsitributiva
1a = a
Propiedad de Identidad
(cd)a = c(da) = d (ca)
Propiedad Aasociativa
Estudio del movimiento
de los cuerpos
Vector de Posición
Posición de algo en el plano cartesiano
o en el espacio
Vector de Desplazamiento
Tiene su punto de origen en el
punto P0 y su extremo en P1
Vector de Velocidad Media
Tiene la misma dirección y sentido
que el vector desplazamiento
Vector de Velocidad
Cociente entre el vector de desplazamiento
y el intervalo de tiempo que empleo el cuerpo
Distancia en 3 dimensiones
La distancia |P1P2| entre los puntos P1(X1,Y1,Z1) y P2(X2,Y2,Z2) es: