CALCULUS I FALL 2013

CHAPTER ONE...The Beginning (of the end)

Pre-Cal Review

Definition of a funtion

for any given x value in a domain there is a unique y value in the range such that f(x) = y.

Absolute Value

lal = a, a> or = 0 and lal = -a, a<0

Binomial Theorem

expanding expressions with large exponents

Used to prove the Power Rule for Differentiation

The Limit

Limits

Theorems

SANDWICH

Example. Find lim x→0 x 2 cos(1 x ) . Hide Solutionsqueeze theoremSince −1≤cos(1 x )≤1 for all x (actually we are interested only in x near 0) then −x 2 ≤x 2 cos(1 x )≤x 2 . Since lim x→0 x 2 =lim x→0 −x 2 =0 then by Squeeze theorem lim x→0 x 2 cos(1 x )=0 .On the figure you can see that x 2 cos(1 x ) is squeezed between x 2 and −x 2 .

INTERMEDIATE VALUE

if there is a continuous function on a closed interval [a,b] and w is any number between f(a) and f(b) then there is a point c in [a,b] where f(c) = w.

Continuity

Discontinuity types

jump

removable

infinite

3 things make a function continuous at a number "c":

f(c) is defined

the limit of f(x) as x approaches that number "c" must exist

the limit of the function must equal the value of the function at that point, i.e. limit f(x) as x approaches c = f(c).

Computations

Addition

Subtraction

Product Rule

Quotient Rule

Epsilon/Delta Proofs & Problems

ALTERNATIVE DEFINITION

f'(x)= f(x) - f(a) _______ x - a

REGULAR DEFINITION

The Derivative

DIFFERENTIATION-the slope of the secant is tending towards the slope of the tangent line

Rates of Change

Average Velocity

Rate of change over an interval

Instantaneous Velocity

Difference Quotient

the slope of the tangent line to a graph at a given point

rate of change at a point

Computations

Addition

Subtraction

Product Rule

Quotient Rule

Power Rule

Chain Rule: f'(g(x))g'(x)

Trig Functions

Increments and Differentials

Linear Approximation

aprroximating the value of a function by using the tangent line

Implicit Differentiation

How to find the derivative of a function whose equation has two variables.

Related Rates

Applications of the Definate Integral

Arc Length and Surfaces of Revolution

determining the length of the graph of a function by using the limit of sums of lengths of line segments

surface area

revolving a line segment or multiple connected line segments (graph of a function) around an axis

uses the definate integral

Volume by Cross Sections

finding the volume of a solid using a cross section with the base of that cross section perpendicular to the x axis

Solids of Revolution

finding the volume of a solid revolved around an axis

Definate Intergal

Washer/Disk method

Cylindrical Shells Method

$Area between functions$

Area between functions

Work/Force

Force exerted by a liquid

Constant Force

Variable Force

Moments and Centers of Mss

Theorem of Pappus

Antiderivatives and Integrals

Indefinite Intergral

Substitution

Change of Variables (limits of integration)

Definate Integral

Reimann Sum

Properties of the Definate Integral

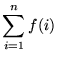
$Summation Notation and Area$

Summation Notation and Area

Finding the area under a curve

Lower Darboux Sum

Upper Darboux Sum

Numerical Integration

Trapezoidal Rule

Simpson's Rule

THEOREMS

Fundamental Theorem of Calculus

Mean Value Theorem of Definate Integrals

Average (mean) Value of Integrals

Applications of the Derivitive

Extrema of Functions

Local and Extreme minimun and maximum values

Critical Values

First Derivitive Test

determines if a function is increasing or decreasing

used to find critical values

Second Derivitive Test

determines concavity

determines if the rate of change of a function is increasing or decreasing

THEOREMS

MEAN VALUE THEOREM

ROLLES THEOREM

Graphing

Optimization

Types of Motion

Rectilinear

Simple Harmonic

Newton's Method

approximating zeros