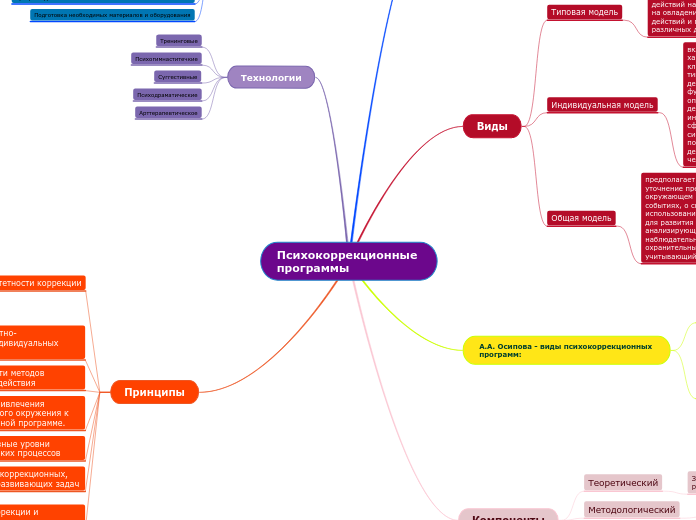
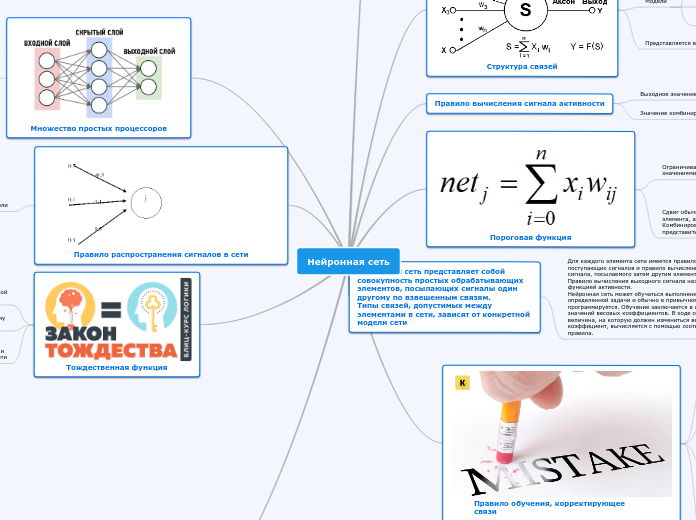
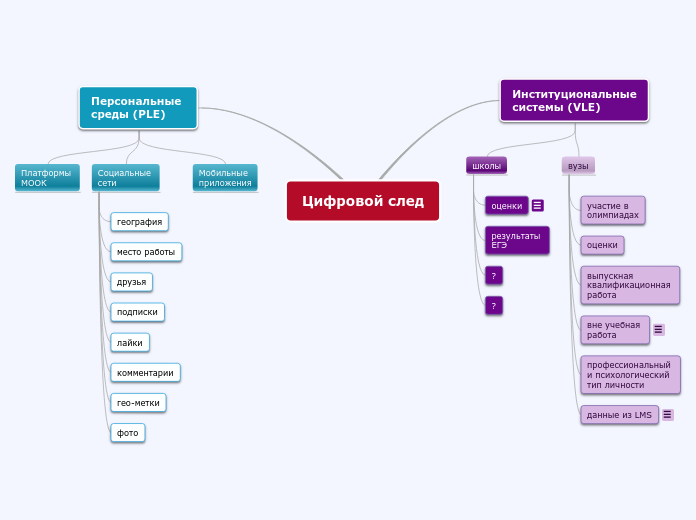
по Bella Prudnikova 7 лет назад
496
регрессионная модель Гретл
Регрессионная модель является инструментом экономико-статистического анализа, который использует уравнения регрессии для связи экзогенных и эндогенных переменных. Основное внимание уделяется числу степеней свободы, которые определяют точность оценки дисперсии ошибки.