по Elsa Noemí Díaz Síntigo 2 лет назад
377
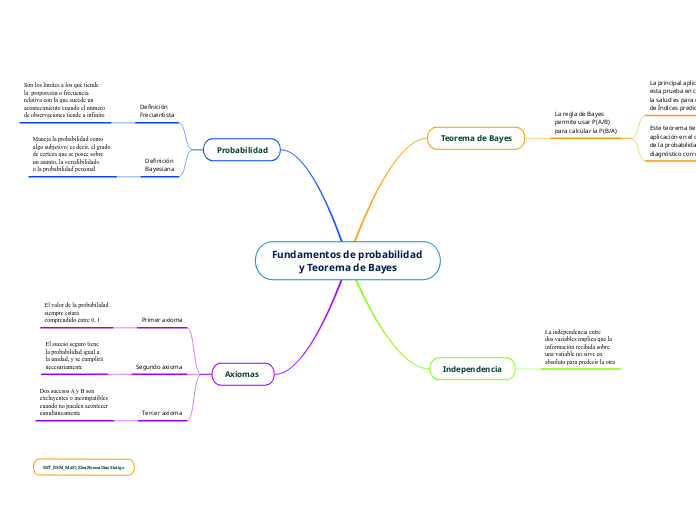
Fundamentos de probabilidad y Teorema de Bayes
по Elsa Noemí Díaz Síntigo 2 лет назад
377

Больше похоже на это