Похідна та її застосування
Похідна́, витвірна́ — основне поняття диференціального числення, що характеризує швидкість зміни функції. Визначається як границя відношення приросту функції до приросту її аргументу коли приріст аргументу прямує до нуля. Функцію, що має скінченну похідну, називають диференційовною.
a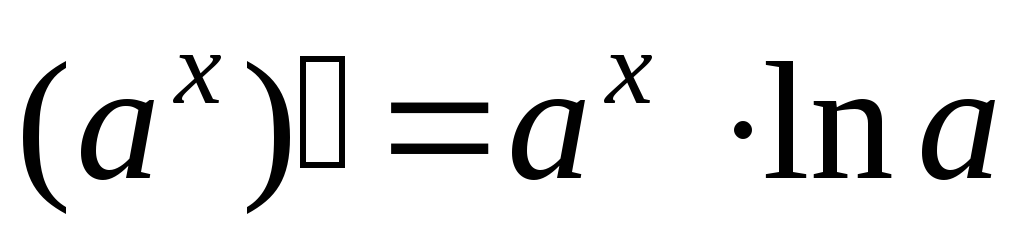
Логарифмічна похідна
Логарифмічна похідна[ред. | ред. ... де f ′ похідна функції f. Коли f функція f(x) від дійсної змінної x, і приймає дійсні, строго додатні значення, логарифмічна похідна дорівнює похідній від ln(f); або, похідній натурального логарифма f.
a
Похідна показникової функції
Похідна показникової функції дорівнює добутку цієї функції на натуральний логарифм її основи.
a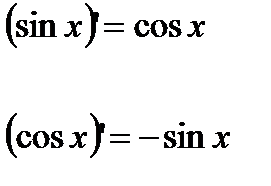
Похідна тригонометричних функцій

Похідна кореня
Перед тим як знаходити похідну кореня, зверніть увагу на інші функції, присутні в вирішуваному прикладі. Якщо в задачі є багато підкореневих виразів, то скористайтеся наступним правилом знаходження похідної квадратного кореня:(√х) '= 1 / 2√х.
a
Похідна частки
В математиці, часткова похідна (частинна похідна) функції кількох змінних — це похідна по одній із змінних, причому інші змінні приймаються як константи. Часткові похідні використовуються у векторному численні та диференційній геометрії.
a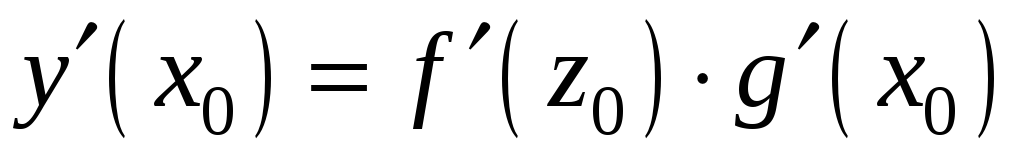
Похідна добутку
Правило добутку — характерна властивість диференціальних операторів, також відома як тотожність Лейбніца.Найважливішим і найпростішим прикладом є диференціювання функцій дійсної змінної. Якщо — дві диференційовні функції, то:Подібна формула справедлива і для голоморфних функцій комплексної змінної.