Трикутник
ТрикутникТрикутник — це фігура, що складається з трьох точок, які не лежать на одній прямій, та трьох відрізків, які сполучають попарно ці точки. Відрізки називають сторонами трикутника, а точки — вершинами трикутника. Кути трикутника, іноді називають внутрішніми кутами трикутника. Кут, суміжний до внутрішнього кута трикутника називають зовнішнім кутом трикутника.Властивості:У будь-якому трикутнику:сума градусних мір кутів трикутника дорівнює 180^\circ;серед внутрішніх кутів принаймні два — гострі;градусна міра зовнішнього кута дорівнює сумі градусних мір двох внутрішніх кутів цього трикутника, не суміжних з ним;зовнішній кут трикутника більший за кожний із кутів трикутника, не суміжних з ним;кожна сторона менша, ніж сума двох інших його сторін;навпроти більшої сторони лежить більший кут;навпроти більшого кута лежить більша сторона;серединні перпендикуляри усіх сторін перетинаються в одній точці (центрі описаного навколо трикутника кола);бісектриса ділить сторону, до якої проведена, на відрізки, пропорційні прилеглим до неї сторонам;усі бісектриси перетинаються в одній точці (центрі вписаного в трикутник кола);усі медіани перетинаються в одній точці, яка ділить кожну із них у відношенні 2:1, рахуючи від вершини трикутника;усі висоти перетинаються в одній точці.
a
Пряма Ейлера
Пряма ЕйлераУ будь-якому трикутнику центр описаного кола, центроїд і ортоцентр лежать на одній прямій. Цю пряму називають прямою Ейлера.
Подібні трикутники
Подібні трикутникиДва трикутники називають подібними, якщо їхні кути відповідно рівні та сторони одного трикутника пропорційні відповідним сторонам другого трикутника. Число, якому дорівнює відношення відповідних сторін, називають коефіцієнтом подібності.Лема про подібні трикутникиПряма, яка паралельна стороні трикутника та перетинає дві інші його сторони, відтинає від даного трикутника йому подібний.Властивості:Відношення периметрів подібних трикутників дорівнює коефіцієнту подібності.Відношення площ подібних трикутників дорівнює квадрату коефіцієнту подібності.

Рівні трикутники
Рівні трикутникиДва трикутники називають рівними, якщо їх можна сумістити накладанням.Основна властивість рівності трикутниківДля даного трикутника ABC і даного променя A_1M існує трикутник A_1B_1C_1, який дорівнює трикутнику ABC, такий, що AB=A_1B_1, BC=B_1C_1, AC=A_1C_1 і сторона A_1B_1 належить променю A_1M, а вершина C_1 лежить у заданій півплощині відносно прямої A_1M.
a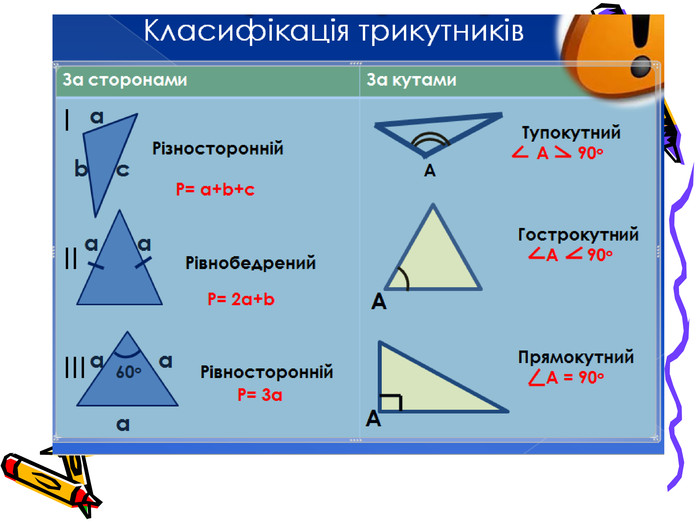
Види трикутників
Види трикутниківЗалежно від довжини сторін розрізняють різносторонні, рівнобедрені і рівносторонні (або правильні) трикутники.Залежно від величини кутів розрізняють гострокутні, прямокутні й тупокутні трикутники.
a
Основні поняття
Чудовими лініями трикутника називають такі відрізки: висота, медіана, бісектриса.

Вписане коло
Вписане колоКоло називають вписаним у трикутник, якщо воно дотикається до всіх сторін цього трикутника.Властивості:У будь-який трикутник можна вписати коло.Центр кола, вписаного в трикутник, лежить на перетині бісектрис цього трикутника.Формула радіуса кола, вписаного в трикутник:r=\dfrac{S}{p}.
a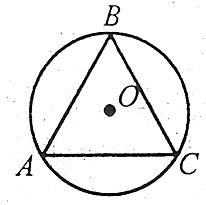
Описане коло
Описане колоКоло називають описаним навколо трикутника, якщо воно проходить через усі його вершини.Властивості:Навколо будь-якого трикутника можна описати коло.Центр кола, описаного навколо трикутника, лежить на перетині серединних перпендикулярів сторін трикутника.Формули радіуса кола, описаного навколо трикутника:R=\dfrac{abc}{4S};R=\dfrac{a}{2\sin{\alpha}} , R=\dfrac{b}{2\sin{\beta}} , R=\dfrac{c}{2\sin{\gamma}} .
a