
Описательная статистика (ОС) - раздел математической статистики предназначенный для представления данных в удобном виде и описания информации в терминах математической статистики и теории вероятностей. Цель ОС — обработка эмпирических данных, их систематизация, наглядное представление в форме графиков и таблиц, а также их количественное описание посредством основных статистических показателей.
ОС дает сжатую и концентрированную характеристику изучаемого явления.
Основные статистические показатели можно разделить на две группы
Меры центральной тенденции (меры среднего уровня) -такие значения признака, вокруг которых группируются отдельные наблюдаемые значения.
Среднее арифметическое (выборочная средняя) – это средняя арифметическая всех вариант в выборке. Является хорошей мерой центральной тенденции для количественных данных, не имеющих выбросов.

Медиана - значение, которое делит упорядоченное множество данных пополам, при этом одна половина значений оказывается больше медианы, а другая – меньше. Медиана подходит для порядковых данных и для количественных данных, в том числе и при наличии выбросов

Мода - это такое значение признака, которое встречается наиболее часто. Мода подходит для номинальных данных.
Меры разброса (меры рассеяния)
Размах измеряет на числовой шкале расстояние, в пределах которого изменяются значения. Это разность максимального и минимального значений выборки.

Квартили – это значения признака, делящие упорядоченную совокупность на четыре равновеликие части.
Выборочная дисперсия – это средняя арифметическая квадратов отклонений вариант от выборочной средней
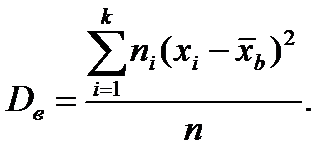
Исправленная выборочная дисперсия описывает то же самое, что и выборочная дисперсия, и вычисляется по формуле

Стандартное отклонение, обозначаемое sx для выборки, равно квадратному корню из исправленной выборочной дисперсии.
Стандартная ошибка (или ошибка средней):

Доверительный интервал - это вычисленный на основе выборки интервал значений признака, который с известной вероятностью содержит оцениваемый параметр генеральной совокупности.

