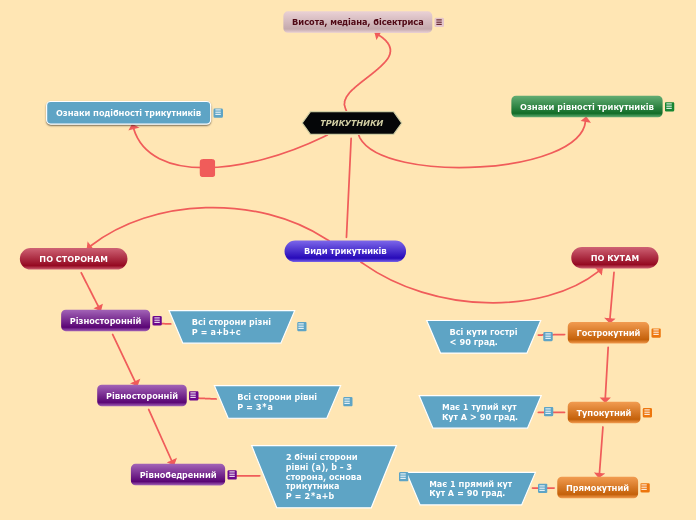
Види трикутників

Різностороннім називається трикутник, у якого всі сторони мають різну довжину. Внутрішні кути різностороннього трикутника різні.

Рівносторонній трикутник — трикутник, усі сторони якого рівні. В Евклідовій геометрії всі три кути рівностороннього трикутника також рівні. Тому рівносторонні трикутники є правильними многокутниками і мають назву правильних. Усі кути правильного трикутника дорівнюють 60° (або ).

Рівнобедрений трикутник — трикутник, в якому дві сторони рівні між собою. Рівні сторони називаються бічними, а остання — основою. За означенням, правильний трикутник також є рівнобедреним, але обернене твердження не є правильним.

Сторона, протилежна до прямого кута, називається гіпотенуза. Інші дві сторони називаються катетами прямокутного трикутника. Тупокутний трикутник має один внутрішній кут більший ніж 90°. В гострокутному трикутнику всі кути менші за 90°.

Сторона, протилежна до прямого кута, називається гіпотенуза. Інші дві сторони називаються катетами прямокутного трикутника. Тупокутний трикутник має один внутрішній кут більший ніж 90°. В гострокутномутрикутнику всі кути менші за 90°.

Прямокутний трикутник — трикутник, один із кутів якого прямий. Прямокутний трикутникзаймає особливе місце в планіметрії, оскільки для нього існують прості співвідношення між сторонами і кутами. Сторони прямокутного трикутника мають власні назви.

 Перша ознака подібності трикутників (за двома кутами)   Якщо два кути одного трикутника відповідно дорівнюють двом кутам другого трикутника, то такі трикутники є подібними.   Друга ознака подібності трикутників (за двома сторонами і кутом між ними)   Якщо дві сторони одного трикутника пропорційні двом сторонам другого трикутника і кути, утворені цими сторонами, рівні, то такі трикутники є подібними.   Третя ознака подібності трикутників (за трьома сторонами)   Якщо три сторони одного трикутника пропорційні трьом сторонам другого трикутника, то такі трикутники є подібними.

Наприклад: трикутники АВС і А1В1С1 – рівні.   Рівність трикутників позначається так: .   Якщо два трикутники рівні, то елементи (тобто сторони, кути, медіани, бісектриси, висоти тощо) одного з них відповідно дорівнюють елементам другого.  Наприклад: , АВ=А1В1, ВС=В1С1, АС=А1С1.   На малюнках рівні відрізки позначаються рівною кількістю рисок, а рівні кути однаковою кількістю дужок. У рівних трикутників проти рівних сторін лежать рівні кути, а проти рівних кутів – рівні сторони.   Перша ознака рівності трикутників (за двома сторонами і кутом між ними)   Якщо дві сторони і кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними другого трикутника, то такі трикутники є рівними.   Друга ознака рівності трикутників (за стороною і двома прилеглими кутами)   Якщо сторона і два прилеглі до неї кути одного трикутника відповідно дорівнюють стороні і двом прилеглим до неї кутам другого трикутника, то такі трикутники - рівні.   Третя ознака рівності трикутників (за трьома сторонами)   Якщо три сторони одного трикутника відповідно дорівнюють трьом сторонам другого трикутника, то такі трикутники є рівними.   Два прямокутні трикутники рівні, якщо виконується одна з умов:два катети одного трикутника відповідно дорівнюють двом катетам другого трикутника;катет і гострий кут одного трикутника відповідно дорівнюють катету і гострому куту другого трикутника;гіпотенуза і гострий кут одного трикутника дорівнюють гіпотенузі і гострому куту другого трикутника;гіпотенуза і катет одного трикутника відповідно дорівнюють гіпотенузі і катету другого трикутника.

Медіана трикутника — це відрізок, що сполучає вершину трикутника із серединою протилежної сторони.Для побудови медіани необхідно виконати такі дії:1) знайти середину сторони;2) з'єднати точку, яка є серединою сторони трикутника, з протилежним відрізком. Це і буде медіана.  У трикутника три сторони, тому можна побудувати три медіани.Усі медіани перетинаються в одній точці.Бісектриса трикутника — це відрізок бісектриси кута трикутника, що сполучає вершину з точкою на протилежній стороні.Для побудови бісектриси необхідно виконати такі дії:1) побудувати бісектрису кута трикутника (бісектриса кута — це промінь, що виходить із вершини кута й ділить його на дві рівні частини);2) знайти точку перетину бісектриси кута трикутника з протилежною стороною;3) з'єднати вершину трикутника з точкою перетину бісектриси кута трикутника з протилежною стороною — цей відрізок і буде бісектрисою трикутника. У трикутника три кути і три бісектриси.Усі бісектриси перетинаються в одній точці.Висота трикутника — це перпендикуляр, опущений із вершини трикутника до прямої, що містить його протилежну сторону.Для побудови висоти необхідно виконати такі дії:1) провести пряму, яка містить одну зі сторін трикутника (у разі, якщо проводиться висота з вершини гострого кута в тупокутному трикутнику);2) із вершини, що лежить навпроти проведеної прямої, опустити до неї перпендикуляр (перпендикуляр — це відрізок, проведений із точки до прямої, який утворює з нею кут величиною 90°). Це і буде висота.Так само, як медіани і бісектриси, трикутник має три висоти.Висоти трикутника перетинаються в одній точці.Але, як згадано вище, для деяких видів трикутників побудова висот і точки їх перетину відрізняються.Якщо трикутник має прямий кут, то сторони, що утворюють прямий кут, можна назвати висотами, оскільки вони перпендикулярні одна до іншої. Точкою перетину висот є спільна вершина перпендикулярних сторін. Якщо трикутник має тупий кут, то висоти, опущені з вершин гострих кутів, знаходитимуться за межами трикутника. Прямі, на яких розташовані висоти, перетинатимуться за трикутником.  Зверни увагу!Якщо з однієї й тієї самої вершини провести медіану, бісектрису й висоту, то медіана виявиться найдовшим відрізком, а висота — найкоротшим.