Álgebra Lineal I
Elementos de un Vector

Expresión Algebraica
de un Vector
Es la coordenada (a,b) que
identifica al vector.

Magnitud de un Vector
Es la medida del vector, y se halla
usando Pitágoras.

Dirección de un Vector
Se refiere al ángulo que
forma el vector con el eje x

Vector Unitario
Es un vector de Magnitud 1
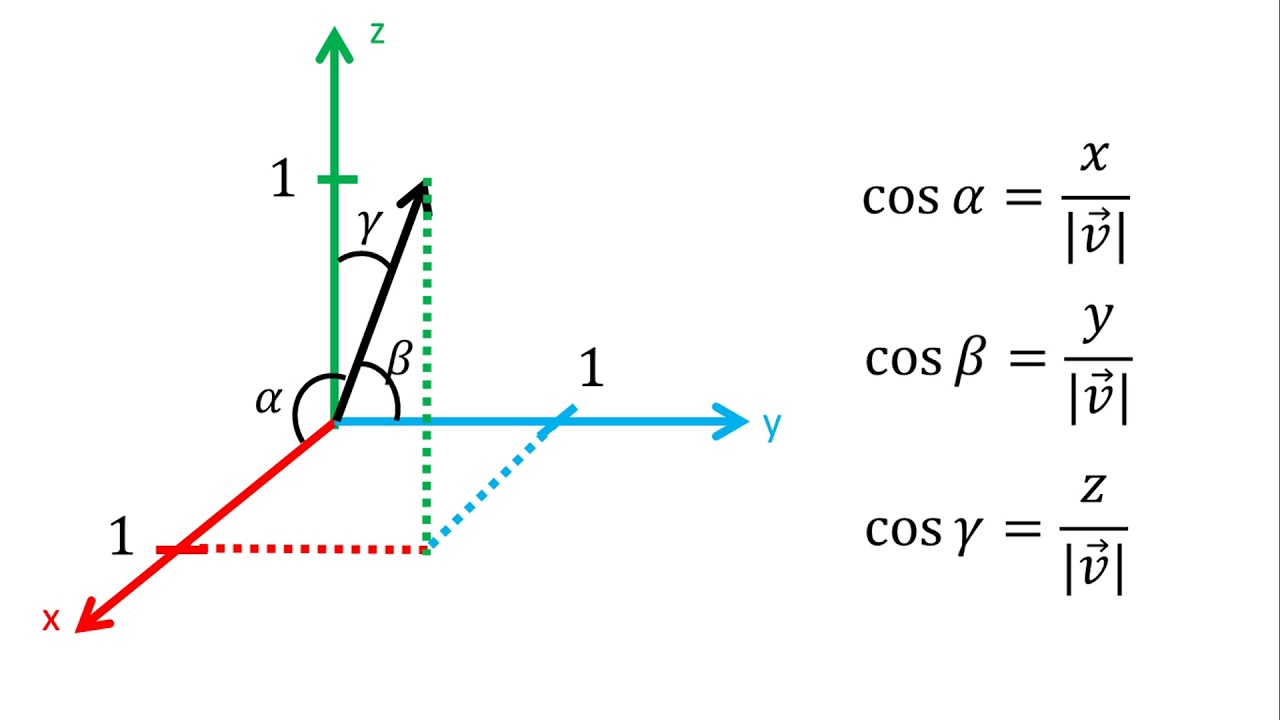
Ángulos Directores
Son los àngulos α, β y γ que forma
el ángulos en las coordenadas
i,j y k respectivamente.
Propiedades de Vectores
Propiedades
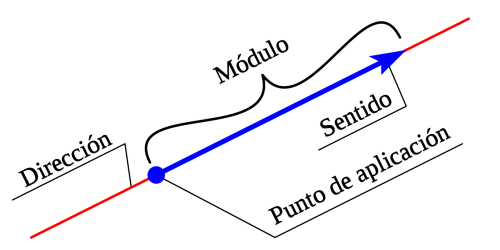
Origen o Punto de Aplicación
Es el punto exacto
donde actúa el vector.
Dirección
Es la recta que lo contiene
o una de sus paralelas.
Módulo o Magnitud
Es la longitud del vector
Sentido
Es determinado por la
flecha en la que termina.
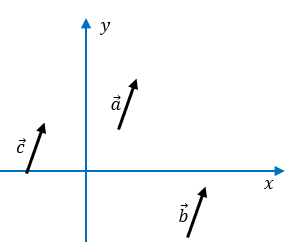
Igualdad de dos vectores
Dos vectores son iguales cuando
coinciden en magnitud, dirección
y sentido.
Propiedades de la Suma de Vectores
Conmutativa
A+B=B+A
Asociativa
(A+B)+C=A+(B+C)
Distributiva
k(A+B)=kA+kB
Inverso Aditivo
A+(-A)=0
Tipos de Vectores
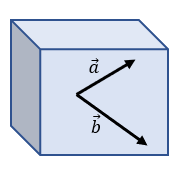
Vectores Coplanares
Están sobre el mismo plano.
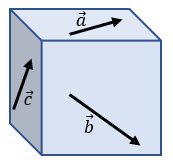
Vectores NO Coplanares
NO están en el mismo plano.
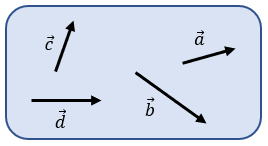
Vectores Libres
No poseen un punto de
aplicación en particular.

Vectores Libres
Se encuentran en la misma
dirección o línea de acción.
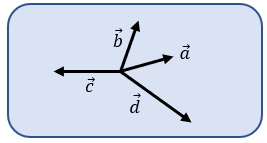
Vectores Concurrentes
o Angulares
Se cruzan en algún punto sobre
la misma dirección o línea de acción.
Forman un ángulo entre ellos.

Vectores BASE
Dos vectores con distinta dirección forman una base. Cualquier vector del plano que forman puede hallarse como composicion lineal de estos.
Operaciones de Vectores
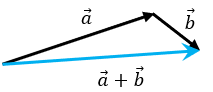
Suma de Vectores
Se realiza gráficamente
o algebraicamente.

Producto por un escalar
Puede multiplicarse un vector
por un escalar positivo o negativo.
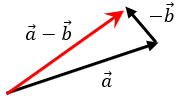
Resta de Vectores
Se realiza con la forma negativa
del vector que se resta.

Producto Punto
El producto de dos vectores, no da
otro vector, sino un escalar.

Producto Vectorial
El resultado del producto cruz es un tercer
vector perpendicular a los dos primeros.
Elementos de una Matriz

Filas de una matriz
Lineas horizontales de la matriz.

Columna de una matriz
Lineas verticales de una matriz.

Orden de la matriz
El orden se denota por m x n donde m son las filas y n las columnas.

Elementos de la matriz
Se denotan por subindices aij donde la i es
el numero de fila, y la j el numero de columna.
Propiedades de Matrices

Propiedades
Determinante
Es un número asociado a la matriz,
y que nos permite saber propiedades
que puede cumplir dicha matriz.
Determinantes n x n

Determinante nxn
Determinante 2x2
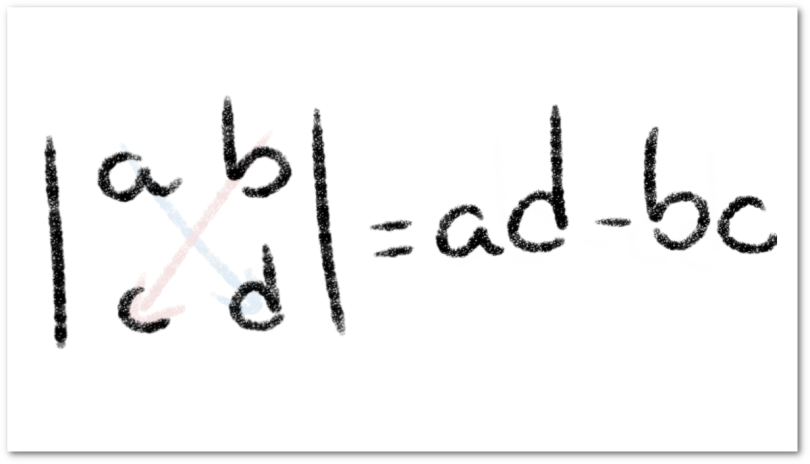
Determinante 2x2
Operaciones de Matrices

Suma de Matrices
Se hace con matrices del mismo orden,
sumando cada elemento respectivo.
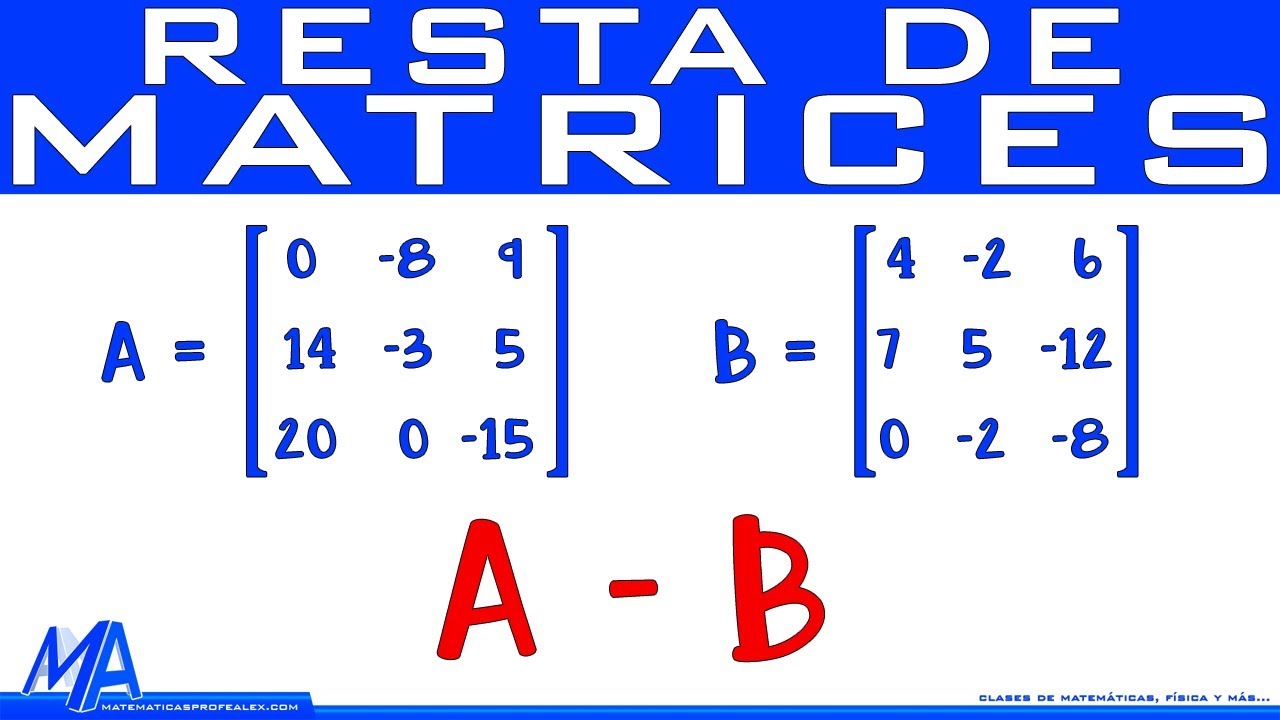
Resta de Matrices
Se realiza con matrices del mismo orden,
restando uno a uno sus componentes.

Multiplicación de Matrices
Se realiza entre una matriz m x n y otra n x m, multiplicando filas por columnas y sumando.

Producto de un escalar de una Matriz
Se multiplica cada elemento
de la matriz por el escalar.
Propiedades de la Suma de Matrices
Conmutativa
A+B=B+A
Asociativa
(A+B)+C=A+(B+C)
k(mA)=km(A)
Distributiva
k(A+B)=kA+kB
(k+m)A=kA+mA
Inverso Aditivo
A+(-A)=(-A)+A=0
Módulo de la Suma
A+O=O+A=A
Módulo del Producto
1A=A
TIPOS DE MATRICES

Matriz Cuadrada
Son matrices de orden n x n
Definite article
Indefinite article

Matriz Rectangular
Son matrices de orden m x n con m distinto de n

Matriz Columna
Matrices con una sola columna.

Matriz Fila
Matrices con una sola fila.

Matriz Diagonal
Es una matriz n x n que solo tiene elementos
en la diagonal principal, y el resto son ceros.

Matriz Escalar
Matriz Diagonal con los elementos de
la diagonal principal todos iguales.

Matriz Triangular
Solo tiene elementos por encima o
por debajo de la diagonal principal.

Matriz Identidad
Es de orden n x n, solo tiene 1 en la
diagonal principal, y el resto son ceros.