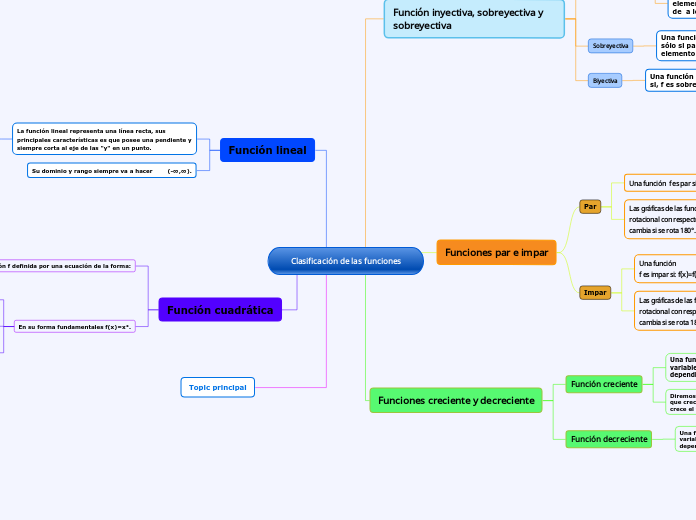
Clasificación de las funciones
Función inyectiva, sobreyectiva y sobreyectiva
Función inyectiva
Una función de A en B es inyectiva, si y sólo si, cualesquiera que sean x1 y x2 Є A, si X1 ≠ X2 entonces, f(X1) ≠ F(x2).
Para que una función sea inyectiva, cada elemento del dominio puede debe ser imagen de a lo sumo un elemento del dominio.
Sobreyectiva
Una función f de A en B es sobreyectiva, si y sólo si para todoy perteneciente a B existe un elemento x perteneciente a A, tal que f(x)=y.
En otras palabras para que una función sea sobreyectiva, el condominio y la imagen deben coincidir.
Biyectiva
Una función f de A en B es biyectiva, si y sólo si, f es sobreyectiva e inyectiva.
Funciones par e impar
Par
Una función f es par si: fx=(-x), ∀x
Las gráficas de las funciones impares presentan simetría rotacional con respecto al origen. Es decir, la gráfica no cambia si se rota 180°.
Impar
Una función
f es impar si: f(x)=f(-x), ∀x
Las gráficas de las funciones impares presentan simetría rotacional con respecto al origen. Es decir, la gráfica no cambia si se rota 180°.undefined
Funciones creciente y decreciente
Función creciente
Una función es creciente cuando al aumentar la variable independiente de x aumenta la variable dependiente y.
Diremos que una función es creciente cuando a medida que crece el valor de la variable independiente
crece el valor de la función.
Función decreciente
Una función es decreciente cuando al aumentar la variable independiente x disminuye la variable dependiente y.
Función lineal
La función lineal representa una línea recta, sus principales características es que posee una pendiente y siempre corta al eje de las "y" en un punto.
Su forma fundamental es: f(x)=X
Su dominio y rango siempre va a hacer (-∞,∞).
Función cuadrática
Una función f definida por una ecuación de la forma:
y=f(x)= ax² + bx +c
Donde a ≠ 0
En su forma fundamentales f(x)=x².
Una función cuadrática es un tipo de función que se caracteriza por ser un polinomio de segundo grado.
La función cuadrática forma una parábola simétrica con el eje vertical.
La función cuadrática siempre estará comprendida en el primer y cuarto cuadrante de una gráfica.