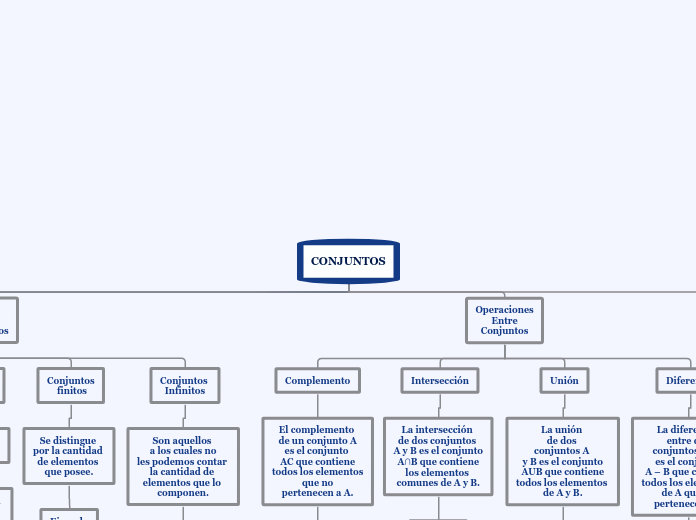
CONJUNTOS
Formas
De
Representar
Diagrama
De
Venn
Se muestra
de forma
Gráfica
Por
Extensión
Enumerando todos
y cada uno de los
elementos que
forman parte de él.
Ejemplo
G= {Danilo,
Vanessa, Oscar}
Por
Comprensión
Enlistando los requisitos,
propiedades o
características necesarias
que tendrán los objetos que
pertenezcan al conjunto
Ejemplo
G= {Alumnos de tu
salón que les
guste bailar}
Tipos
De
Conjuntos
Conjunto
universal
Conjunto
formado
por todos
los objetos
de estudio.
Por esta razón
Se representa
con la
letra U.
Ejemplo
A= {1,2,3}
B= {-1,0,4,5}
U= {-1,0,1,2,3,4,5}
Conjunto
vacío
Conjunto
que
no tiene
elementos
Ejemplo
A= { }
Conjuntos
unitarios
Solo tiene
un elemento.
Se representa
con algo que
distinga a ese
conjunto.
Ejemplo
A= {manzana}
Conjuntos
finitos
Se distingue
por la cantidad
de elementos
que posee.
Ejemplo
A= {a,e,i,o,u}
Z= {x/x es
una palabra}
Conjuntos
Infinitos
Son aquellos
a los cuales no
les podemos contar
la cantidad de
elementos que lo
componen.
Ejemplo
P= {a/a es par}
Q= {0,3,6,9,…}
Operaciones
Entre
Conjuntos
Complemento
El complemento
de un conjunto A
es el conjunto
AC que contiene
todos los elementos
que no
pertenecen a A.
Ejemplo
U= {1,2,3,4,5,6,7,8}
A= {1,3,4,7,8}
A´= {2,5,6}
Intersección
La intersección
de dos conjuntos
A y B es el conjunto
A∩B que contiene
los elementos
comunes de A y B.
Ejemplo
La intersección
de los
conjuntos {1,2,3}
y {2,3,4}
es {2,3}
Unión
La unión
de dos
conjuntos A
y B es el conjunto
AUB que contiene
todos los elementos
de A y B.
Ejemplo
A= {a,b,c,d}
B= {d,e,f}
AUB= {a,b,c,d,e,f}
Diferencia
La diferencia
entre dos
conjuntos A y B
es el conjunto
A – B que contiene
todos los elementos
de A que no
pertenecen a B
Ejemplo
A= {1,2,4,6,7,8,9}
B= {1,2,4,6}
A – B= {7,8,9}
Propiedades
De Los
Conjuntos
Distributiva
AU {B∩C}
= {AUB} ∩ {AUC}
Identidad
AUØ = A
A∩U = A
A∩Ø = Ø
Idempotencia
A∩A = A
AUA = A
Conmutativa
AUB = BUA
Asociativa
AU {BUC}
= {AUB} UC
Morgan
{AUB}´ = A´∩B
{A∩B}´ = A´UB´