CONOCIMIENTOS BÁSICOS
PENSAMIENTO NUMÉRICO Y SISTEMAS NÚMERICOS
se adquiere
Gradualmente
y va
Evolucionando
en la medida que
El estudiante
piensa en los
Números
y los usa en
Contextos significativos
en los
Estándares curriculares
y de
Evaluación
para la
Educación Matemática
el sentido
Númerico
surge de diversos
Significados del número
el autor
Mcintosh (1992)
afirma que el
Pensamiento númerico
que tiene una
Persona
sobre los
Números y operaciones
con la
Habilidad y comprensión
para hacer
Juicios matemáticos
Estrategias
al manejar
Números
Operaciones
se clasifica en
Comprensión de los números y de la numeración
construcción por parte de
Estudiantes
de los
Significados numericos
a partir de
Experiencias cotidianas
y la construcción de
El sistema de numeración
teniendo en cuenta
Actividades
como
Contar
Agrupar
Valor posicional
Comprensión del concepto de las operaciones
reconoce el significado de
La Operación
en
Situaciones concretas
emerge de
Modelos mas usuales
y
práctico de operaciones
además comprende
Las propiedades matemáticas
el efecto y la relación de cada
Operación y entre operaciones
entre ellas tenemos
Adición
Sustracción
Multiplicación
División
Cálculos con números y aplicaciones de números y operaciones
la finalidad de
Los cálculos
es la
Resolución de problemas
por ello concierne que
El docente
estimule a los
Estudiantes
para que
Exploren e inventen estrategias
alternativas para el
Cálculo
sus tipos de decisiones son
la
Comprensión
entre el
Contexto del problema
y el
Cálculo es necesario
una
Conciencia
de que existen varias
Estrategias
para efectuar el
Cálculo
una
Inclinación
a escoger una
Estrategia eficiente
y a revisar
Datos y resultados
PENSAMIENTO ESPACIAL Y SISTEMAS GEOMÉTRICOS
el autor
Howar Gardner
plantea que el
Pensamiento espacial
es esencial para el
Pensamiento Cientifico
es usado para
manipular y representar
la
Información en el aprendizaje
y la
Resolución de problemas
Manejo de información espacial
para
resolver problemas
Orientación, ubicación
y
Distribución del espacio
es peculiar a
Personas
que tienen desarrollada su
Inteligencia espacial
en los
Sistemas geométricos
se hace énfasis en
El pensamiento espacial
considerado como el
Conjunto de procesos cognitivos
en donde se contruyen
Representaciones mentales
de los
objetos del espacio
las
relaciones, transformaciones
y diversas traducciones a
Representaciones materiales
se construyen a través de
La exploración activa
y la
Modelación del espacio
tanto para la situación de
Objetos en reposo
como para el
Movimiento
influenciado por las
Características individuales
como por el
Entorno físico, social, cultural
e
Histórico
se trata de argumentar
El espacio
ayudándose de
Modelos y figuras
con
Palabras del lenguaje ordinario
Gestos
Movimientos Corporales
se clasifican en
Geometría activa
Cuerpos, superficies y lineas
Ángulo
Desarrollo del pensamiento geométrico
Representación bidimensional del espacio tridimensional
Las transformaciones
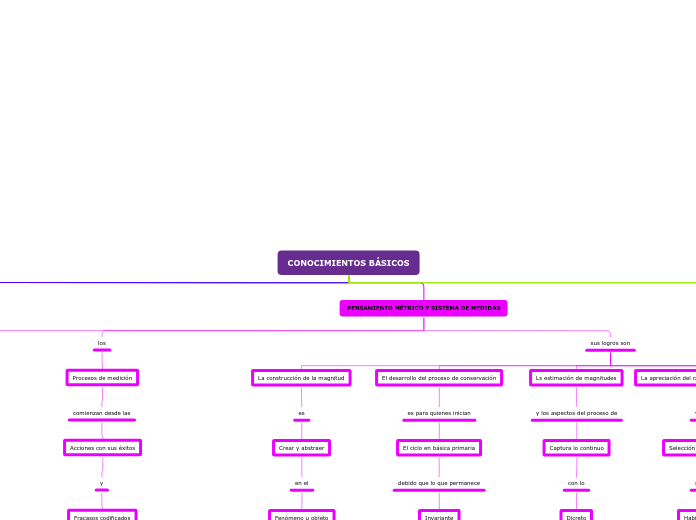
PENSAMIENTO MÉTRICO Y SISTEMA DE MEDIDAS
el proceso de
Medir entre el entorno
y los
Estudiantes
hace que encuentren
Situaciones de utilidad
y
Aplicaciones prácticas
los
Procesos de medición
comienzan desde las
Acciones con sus éxitos
y
Fracasos codificados
en
Clasificaciones
relacionadas con
Imágenes espaciales
esto es con
Modelos geométricos
aún en el caso del
Tiempo
como
Más o menos
Mucho o poco
Grande o pequeño
sus logros son
La construcción de la magnitud
es
Crear y abstraer
en el
Fenómeno u objeto
la
Magnitud concreta
o la
Cantidad susceptible
de
Medición
El desarrollo del proceso de conservación
es para quienes inician
El ciclo en básica primaria
debido que lo que permanece
Invariante
a pesar de alteraciones de
Espacio y tiempo
es imprescindible al conciliar
Conceptos
de
Longitud
Área
Volumen
Peso
Ls estimación de magnitudes
y los aspectos del proceso de
Captura lo continuo
con lo
Dicreto
relacionados con los conceptos
Medida
Conteo
La apreciación del rango de la magnitudes
y la
Selección de unidades
son
Habilidades
poco
Desarrolladas
en los
Niños y adultos
debido al
Tratamiento libresco
y
Descontextualizado
que se le da a
La medición
La selección de unidades
no es necesario
Seleccionar unidades
en un proceso de
Medición
puede terminar con la
Ubicación
de la
Cantidad
en un
Rango de magnitudes
y en la
Afirmación o negación
de una
Comparación
conocida de la misma
Magnitud
El trasfondo social de la medición
la
Interacción social
y la referencia a
Un trasfondo significativo
e importante para el
Estudiante
son insustituibles para construir
Procesos de la medición
en el
Cerebro
de cada uno de
Los participantes
PENSAMIENTO ALEATORIO Y SISTEMA DE DATOS
la
Teoria de la probabilidad
y su aplicación a
Los fenómenos aleatorios
han construido un
Andamiaje matemático
que de alguna manera domina
Acertadamente la incertidumbre
las
Investigaciones de Shanghnessy
establecen que
El pensamiento aleatorio
los
Contenidos de la probabilidad
y la
Estadística
debe tener un
Espíritu de exploración
tanto por parte de
Los estudiantes
Los docentes
el autor
Heinz Steinbring
presenta un
Modelo
basado en un
Análisis epistemológico
de la
Naturaleza de la probabilidad
el cual considera
Tres niveles
como
Estructura
del
Contenido
Aprendizaje significativo
El docente
Planifica
Organiza
apoya
el
Consejo escolar
de
Educación estadística
establece los
Principios
para introducir conceptos como
Los conceptos y técnicas
deben introducirse en
Un contexto práctico
No desarrollar las técnicas
completamente si es por
Primera vez que las presenta
No es necesaria
una
Justificación teórica completa
de todos los
Temas
PENSAMIENTO VARIACIONAL Y SISTEMAS ALGEBRAICOS Y ANALÍTICOS
puede ser iniciado en
El currículo
de
Matemáticas
la
Variación
puede establecerse a partir de
Situaciones problemáticas
cuyo escenarios se refieran a
Fenómenos de cambio
Variación
de la
Vida práctica
presupone supera la
La enseñanza
de
Contenidos matemáticos fragmentados
y
Compartimentalizados
para ubicarse en un
Campo conceptual
que involucra
Conceptos y procedimientos
vinculados que permitan
Analizar
Organizar
Modelar
las
Situaciones
y
Problemas
Actividad práctica
del
Hombre
Ciencias
los
Núcleos conceptuales matemáticos
son
La función como dependencias
y
Modelos de función
Las magnitudes
El Álgebra
en su sentido
Simbólico
liberada de su
Significación geométrica
particularmente la
Noción
Significado de laVariable
Modelos matemáticos
de tipos de
Variación
como
Aditiva
Multiplicativa
Variación
para medir el
Cambio absoluto
Cambio relativo
entre los diferentes
Sistemas de representación
asociados con la
Variación
tenemos
Enunciado verbales
Las representaciones tabulares
Las gráficas de tipo cartesiano
Representaciones pictoricas e iconicas
La instruccional
La mecánica
Fórmulas
Expresiones analíticas
Patrones aditivos y multiplicativos